Question

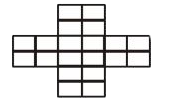
Five crosses are to be put into eleven square blocks written in the form of an E as shown in figure so that every row has a cross. In how many different ways can it be done?

Explanation

To solve the problem of placing 5 crosses into 11 square blocks arranged in the form of an "E" such that every row has one cross, we can break down the solution into clear steps:

1. Identify the Structure:
The "E" shape consists of 5 rows with the following distribution of blocks:
- Row 1: 3 blocks
- Row 2: 1 block
- Row 3: 3 blocks
- Row 4: 1 block
- Row 5: 3 blocks

2. Determine Cross Placement:
We need to place exactly one cross in each of the 5 rows. This means:
- In Row 1, we can choose any of the 3 blocks.
- In Row 2, we have only 1 block, so the cross must go there.
- In Row 3, we can again choose any of the 3 blocks.
- In Row 4, we have only 1 block, so the cross must go there.
- In Row 5, we can choose any of the 3 blocks.

3. Calculate the Number of Ways:
- For Row 1, the number of ways to place the cross = \( \binom{3}{1} = 3 \)
- For Row 2, the number of ways to place the cross = \( \binom{1}{1} = 1 \)
- For Row 3, the number of ways to place the cross = \( \binom{3}{1} = 3 \)
- For Row 4, the number of ways to place the cross = \( \binom{1}{1} = 1 \)
- For Row 5, the number of ways to place the cross = \( \binom{3}{1} = 3 \)

4. Combine the Choices:
The total number of ways to arrange the crosses is the product of the number of choices for each row:
\( \text{Total Ways} = \binom{3}{1} \times \binom{1}{1} \times \binom{3}{1} \times \binom{1}{1} \times \binom{3}{1} = 3 \times 1 \times 3 \times 1 \times 3 \)

5. Calculate the Final Result:
\( \text{Total Ways} = 3 \times 1 \times 3 \times 1 \times 3 = 27 \)

Thus, the total number of different ways to place the crosses is 27.