Let the complex numbers z of the form x+iy satisfy arg(3z−6−3i2z−8−6i)=π4and|z−3+i|=3. Then the ordered pairs (x,y) are (A) (4−4√5,1+2√5) (B) (4+5√5,1−2√5) (C) (6−1) (D) (0,1)
Step by step video & image solution for Let the complex numbers z of the form x+iy satisfy arg ((3z-6-3i)/(2z-8-6i))=pi/4 and |z-3+i|=3. Then the ordered pairs (x,y) are (A) (4- 4/sqrt(5), 1+2/sqrt(5)) (B) (4+5/sqrt(5),1-2/sqrt(5)) (C) (6-1) (D) (0,1) by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
Knowledge Check
The complex numbers z = x + iy which satisfy the equation ∣∣∣z−5iz+5i∣∣∣=1, lie on
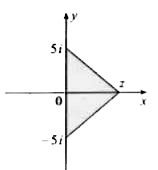 Athe x - axisBthe straight line y = 5Ca circle passing through originDNone of these
Athe x - axisBthe straight line y = 5Ca circle passing through originDNone of theseThe complex numbers z = x + iy which satisfy the equation ∣∣∣z−5iz+5i∣∣∣=1, lie on
 Athe x-axisBthe straight line y = 5Ca circle passing through the originDnone of these
Athe x-axisBthe straight line y = 5Ca circle passing through the originDnone of these
Number of z, which satisfy Arg(z−3−2i)=π6 and Arg(z−3−4i)=2π3 is/are :
View SolutionThe locus of a complex number z satisfying |z−(1+3i)|+|z+3−6i|=4
View SolutionLet z be a complex number and i=√−1 then the number of common points which satisfy arg(z−1−i)=π6 and arg(z−1−iz+1−i)=π2 is
View SolutionIf arg(z−3+4iz+2−5i)=5π6, then locus of z represents ..........
View SolutionThe number of values of z satisfying both theequationsArg(z−1−i)=−3π4 and Arg(z−2−2i)=π4 is
View SolutionLet z1=(1+√3i)2(√3−i)1−iandz2=(√3+i)2(1−√3i)1+i then
View Solution