Show that the reflection of the line px+qy+r=0 in the line x+y+1 =0 is

If r is the geometric mean of p and q, then the line $p x + q y + r = 0$
Ahas a fixed direction
Bpasses thorugh a fixed point
Cforms with the axs a triangle of constant area
Dsum of its intercepts on the axes is constant
The locus of the orthocentre of the triangle formed by the lines $(1 + p) x - p y + p (1 + p) = 0$
$(1 + q) x - q y + q (1 + q) = 0$ and $y = 0$ where $p \neq q$ is
Aa hyperbola
Ba parabola
Can ellipse
Da straight line
Shown below are the graphs of the lines $y - 2 x = 0, x + y = 6 and p x + q y = r$

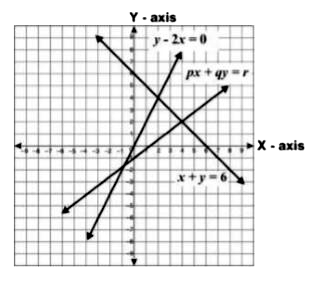
Which of these is the solution for the pair of equations x+y=6 and px+qy=r
Ax=2,y=4
Bx=4, y=2
Cx=3, y=2
DWe cannot say for sure as the values of p and q are not known.

Show that the reflection of the line $p x + q y + r = 0$ in the line $x + y + 1 = 0$ is the line $q x + p y + (p + q - r) = 0,$ where $p \neq - q$ .