Angle of intersection of two circle having distance between their centres d is given by : (A) cosθ=r21+r22−d2r21+r22 (B) secθ=r21+r22+d22r1r2 (C) secθ=2r1r2r21+r22−d2 (D) none of these
To solve the problem of finding the angle of intersection of two circles given the distance between their centers d and their respective radii r1 and r2, we can apply the cosine rule in the triangle formed by the centers of the circles and their point of intersection.
1. Identify the Triangle:
We have two circles with centers C1 and C2 and radii r1 and r2 respectively. The distance between the centers C1 and C2 is d. The points of intersection of the circles can be denoted as point P.
2. Draw the Normals:
At point P, draw the normals to both circles. The normal from C1 to point P and the normal from C2 to point P will meet at point P.
3. Apply the Cosine Rule:
In triangle C1PC2, we can use the cosine rule to find cosθ, where θ is the angle of intersection at point P:
cosθ=r21+r22−d22r1r2
4. Rearranging the Cosine Rule:
From the cosine rule, we can rearrange the equation to express secθ:
secθ=1cosθ=2r1r2r21+r22−d2
5. Final Result:
Therefore, the expression for secθ is:
secθ=2r1r2r21+r22−d2
This matches option (C) from the given choices.
Conclusion:
The correct answer is option (C):
secθ=2r1r2r21+r22−d2
We have two circles with centers C1 and C2 and radii r1 and r2 respectively. The distance between the centers C1 and C2 is d. The points of intersection of the circles can be denoted as point P.
At point P, draw the normals to both circles. The normal from C1 to point P and the normal from C2 to point P will meet at point P.
In triangle C1PC2, we can use the cosine rule to find cosθ, where θ is the angle of intersection at point P:
cosθ=r21+r22−d22r1r2
From the cosine rule, we can rearrange the equation to express secθ:
secθ=1cosθ=2r1r2r21+r22−d2
Therefore, the expression for secθ is:
secθ=2r1r2r21+r22−d2
This matches option (C) from the given choices.
The correct answer is option (C):
secθ=2r1r2r21+r22−d2
Similar Questions
Knowledge Check
1r21+1r22+1r23+1r2=
Aa2+b2+c2s2BΣa2S2C4RD4RThe distance between the centres of the two circles of radii r1 and r2 is d. They will thouch each other internally if
Ad=r1orr2Bd=r1+r2Cd=r1−r2Dd=√r1r2The distance between the centres of the two circles of radii,r1 and r2 is d. They will touch each other internally if
Ad=r1orr2Bd=r1+r2Cd=r1−r2Dd=√r1r2
The total surface area of frustum shaped glass tumbler is (r1>r2) <br> (a) πr1l+πr2l <br> (b) πl(r1+r2)+π(r2)2 <br> (c) 13πh((r1)2+(r2)2+r1r2) <br> (d) √h2+(r1−r2)2
View SolutionIf the sum of the areas of two circles with radii r1 and r2 is equal to the area of a circle of radius r, then r21+r22 (a) >r2 (b) =r2 (c) <r2 (d) None of these
View SolutionIn the given loop the magnetic field at the centre O is
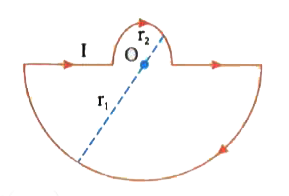
1) μ0I4(r1+r2r1r2) out of the page
2) μ0I4(r1+r2r1r2) into the page
3) μ0I4(r1−r2r1r2) out of the page
4) μ0I4(r1−r2r1r2) into the page
View SolutionIf rr1=r2r3, then A=900 (b) B=900 C=900 (d) none of these
View SolutionShow that 16R2rr1r2r3=a2b2c2
View Solution
