If n forces −−→PA1……−−→PAn divege from point P and other forces −−−→A1Q,−−−→A2Q,.,−−−→AnQ vonverge to point Q , then the resultant of the 2n forces is represent in magnitude and directed by (A) n−−→PQ (B) n−−→QP (C) 2n−−→PQ (D) n2−−→PQ
Step by step video & image solution for If n forces vec(PA)_1 ……vec(PA)_n divege from point P and other forces vec(A_1Q),vec(A_2Q), ., vec(A_nQ) vonverge to point Q , then the resultant of the 2n forces is represent in magnitude and directed by (A) nvec(PQ) (B) nvec(QP) (C) 2n vec(PQ) (D) n^2vec(PQ) by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
Forces −−→PA.−−→PB and vec(PC)÷er≥omthep∮Pandotherforcesvec(AQ), vec(BQ),vec(CQ)conver≥→ap∮Q.Showtˆtherestant–––––ofsixsixforcesisrepresented∈magnitudeanddirectionbye3vec(PQ)
View SolutionThe three vectors →A,→Band→C are repesented in magnitude and direction by −−−−−−−→OP,−−→OQ, show that (S) is the mid point of (PQ).
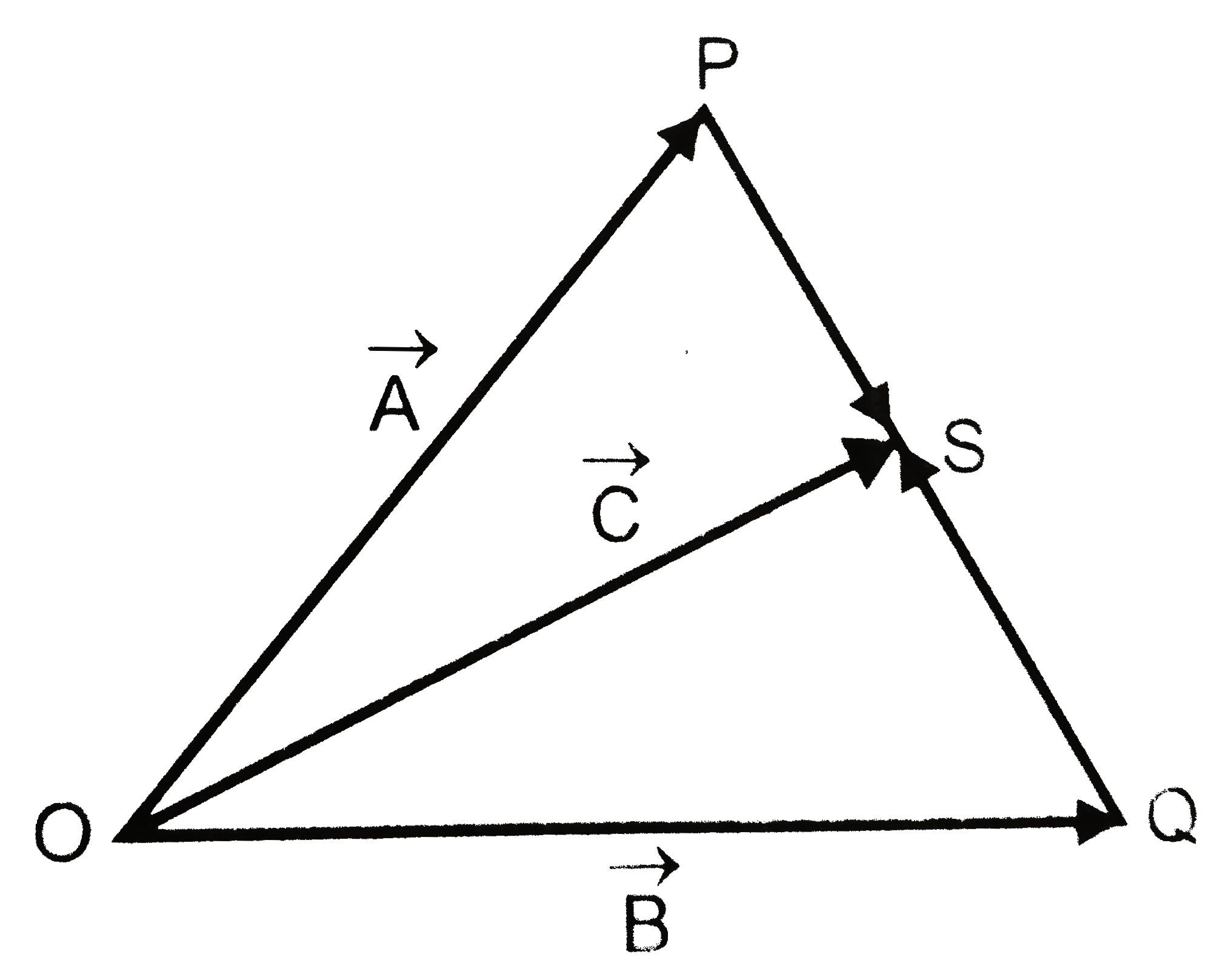 .
.
View Solution
Knowledge Check
If a force →F=(→i+2→j+→k)N acts on a body produces a displacement of →S=(4→i+→j+7→k)m, then the work done is
A9JB13JC5JD1JThe position vectors of P and Q are respectively →aand→b. If R is a point on −−→PQ such that −−→PR=5−−→PQ, then the position vector of R, is
A5→b−4→aB5→b+4→aC4→b−5→aD4→b+5→aLet the vectors −−→PQ,−−→QR,−−→RS,−→ST,−−→TU and −−→UP represent the sides of a regular hexagon.
Statement 1: −−→PQ×(−−→RS+−→ST)≠→0
Statement 2: −−→PQ×−−→RS=→0 and −−→PQ×−→ST≠→0A1B2C3D4
Find magnitude and direction of →F2−→F1 if →F1=500N due east and →F2=250N due north:
View SolutionThe sum of two forces →P and →Q is →R such that ∣∣→R∣∣=∣∣→P∣∣ .The angle θ (in degrees) that the resultant of 2→P and →Q will make with →Q is
View SolutionThe resultant vector of →P and →Q is →R. On reversing the direction of →Q, the resultant vector becomes →S. Show that : R2+S2=2(P2+Q2)
View SolutionIf P(2,3,-6) and Q(3,-4,-6) are two points in the space. Find the direction cosines of −−→OP,−−→QO and −−→PQ, where Q is the origin.
View SolutionTwo vector →P and →Q act at a point and have a resultant R1.Ifvec Qisreplacedbythevev→r ( vec (R_1^2-P^2)/Qshowthtthereatant–––––isstillofmagnitude vec R_1.
View Solution
