In a circle with centre O,chords AB and CD intersect inside the circumference at E.Prove that ∠AOC+∠BOD=2∠AEC
∠AOC=2∠ABC
∠AOC=2∠EBC−(1)
∠BOD=2∠BCD
∠BOD=2∠BCE−(2)
adding equation 1 and 2
∠AOC+∠BOD=2(∠EBC+∠BCE
In∠EBC
∠BEC=1800−∠EBC−∠BCE
∠AOC+∠BOD=2(1800−∠EBC)=2∠AEC.
Similar Questions
Knowledge Check
In a circle with centre O, chords AB and CD intersect inside the circumference at E. Find ∠AEC. If ∠AOC=40∘and∠BOD=50∘.
A90∘B45∘C30∘D60∘
In a circle with centre O, chords ABandCD intersect inside the circumference at E. Prove that ∠AOC+∠BOD=2∠AEC.
View SolutionIn a circel with centre O. chords AB and CD interest inside the circumference at E. Prove that ∠AOC+BOD=2∠AEC.
View SolutionIn a cricle, two chords AB and CD intersect at a point P inside the circle. Prove that
(a)ΔPAC~ΔPDB (b)PA⋅PB=PC⋅PD.
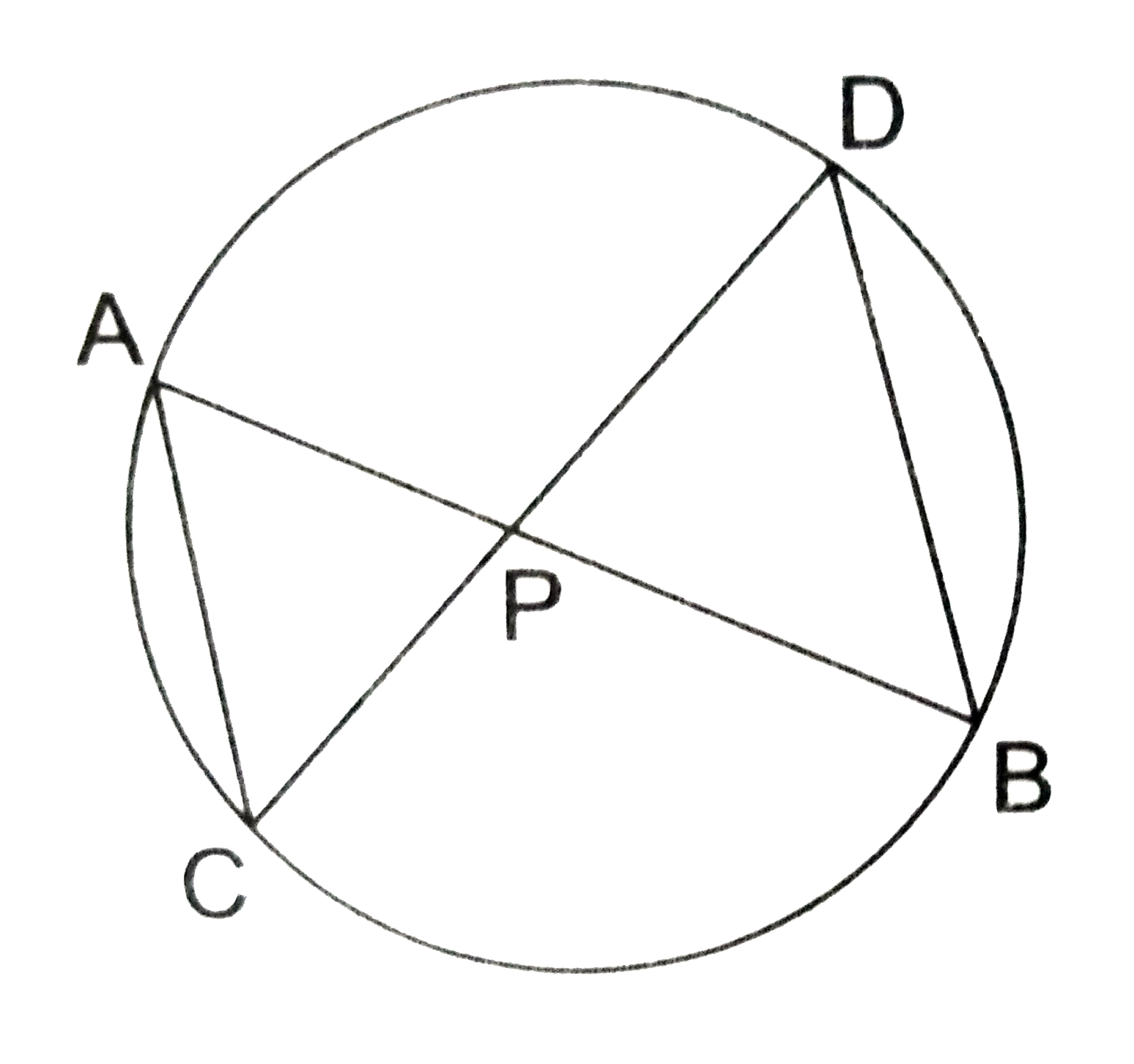
View SolutionTwo equal chord AB and CD of a circle with centre O, intersect each other at point P inside the circle.

Prove that:
BP=DP
View SolutionThe equal chords AB and CD of circle with centre O, when produced, meet at P outside the circle. Prove that :
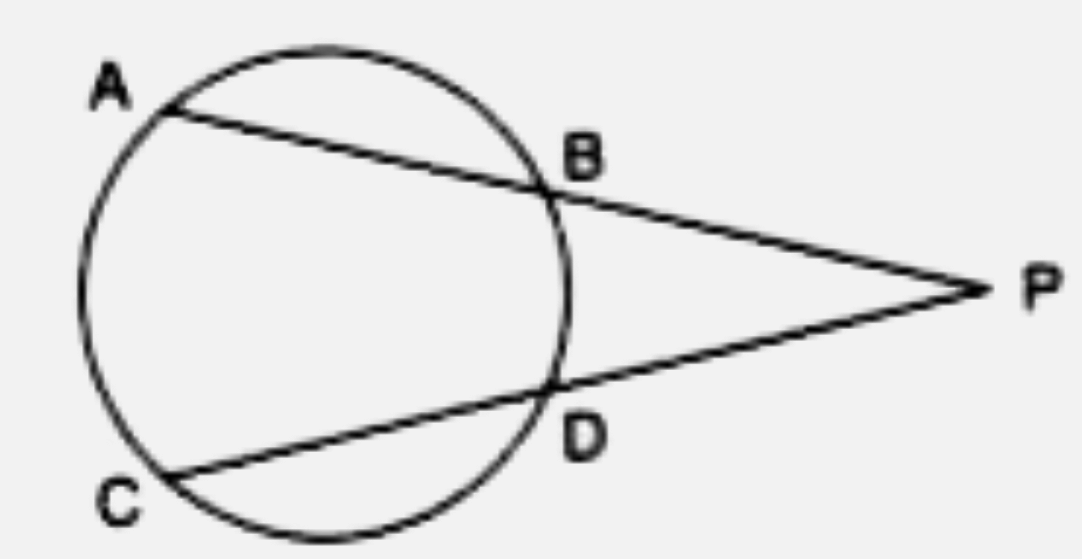
PA=PC.
View SolutionCommon tangents AB and CD to two circles intersects at E. Prove that AB=CD
View SolutionThe equal chords AB and CD of circle with centre O, when produced, meet at P outside the circle. Prove that :

PB=PD
View Solution
