दिखाइए x=2,y=1 समीकरण 7x+4y=18 को संतुष्ट करते है|
x=2,y=1 दिए समीकरण को L.H.S में रखने पर
L.H.S.=7×2+4×1=18=R.H.S.
∴x=2 और y =1 दी रैखिक समीकरण को संतुष्ट करते है|
Topper's Solved these Questions
- दो चरों वाले रैखिक समीकरण BOOK - NOOTAN HINDICHAPTER - दो चरों वाले रैखिक समीकरण EXERCISE - प्रश्नावली
8 Videos
- दो चरों वाले रैखिक समीकरण BOOK - NOOTAN HINDICHAPTER - दो चरों वाले रैखिक समीकरण EXERCISE - प्रश्नावली 4.1
2 Videos
- त्रिभुज BOOK - NOOTAN HINDICHAPTER - त्रिभुज EXERCISE - विविधि प्रश्नावली ( दीर्घ उत्तरीय प्रश्न )
8 Videos
- निर्देशांक ज्यामिति BOOK - NOOTAN HINDICHAPTER - निर्देशांक ज्यामिति EXERCISE - विविध प्रश्नावली
8 Videos
Similar Questions
निम्नलिखित प्रत्येक समीकरण का आलेख बनाइए:
(i) x=4 (ii)x−6=0 (iii)x+3=0 (iv)y=2 (v)2x−5=0 (vi)y+3=0
View Solutionएक नोटबुक की कीमत एक कलम की कीमत से दोगुनी है| इस कथन को निरूपित करने के लिए दो चरो वाला एक रैखिक समीकरण लिखिय|
[संकेत: मान लीजिए,नोटबुक की कीमत रु x है और कलम की कीमत रु y है]
View Solutionदी आकृति में, यदि x = y और AB = CB है, तो सिद्ध कीजिए कि AE = CD है।
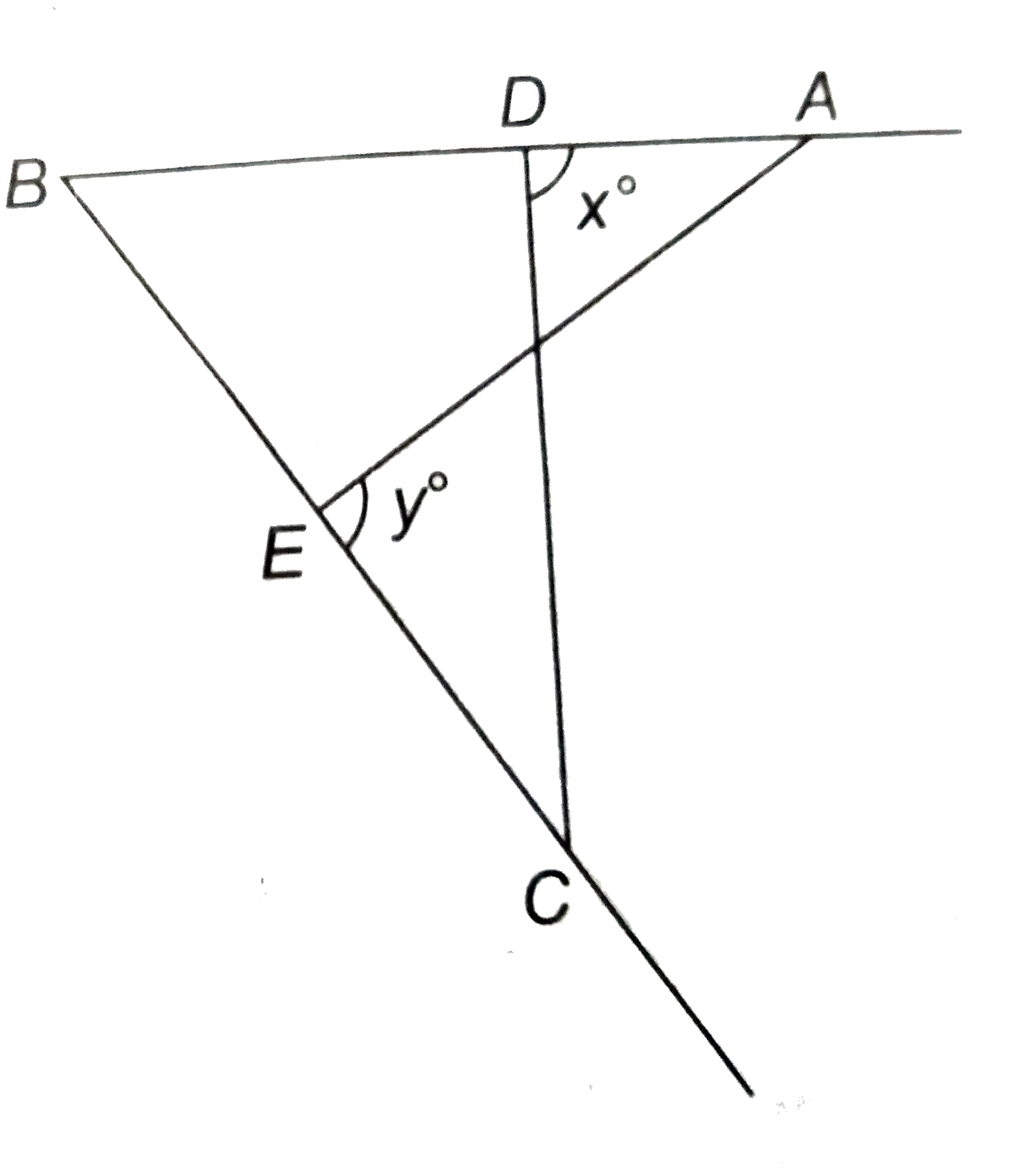
View Solutionमूल बिन्दु के निर्देशांक लिखिए |
View SolutionShow that x=2,y=1, satisfy the linear equation 7x+4y=18
View Solutionयदि θ और ϕ न्यूनकोण है sinθ=1/2cosϕ=1/3 को संतुष्ट करते है ,तब θ+ϕ∈:
View Solutionसिद्ध कीजिए कि बिंदुओं (2,3) और(3,4) को मिलाने वाले रेखाखण्ड के मध्य बिंदु के निर्देशांक x और y निम्नलिखित समीकरण को संतुष्ट करते है :
x−y+1=0.
View Solutionदिखाइए कि y=esin−1x अवकल समीकरण (1−x2)d2ydx2−xdydx=y का हल है |
View Solutionदिखाइए कि फलन y=ax2+bx अवकल समीकरण x2d2ydx2−2xdydx+2y=0 का हल है |
View Solution1 से 5 में अचरों a व b को विलुप्त करते हुए दिये वक्रों के कुल को निरूपित करने वाला अवकल समीकरण ज्ञात कीजिए-
xa+yb=1
View Solutionदिखाइए कि y2=a(x+b) अवकल समीकरण yd2ydx2+(dydx)2=0 का हल है |
View Solutionदिखाइए कि फलन y=k(x−k)2 अवकल समीकरण (dydx)3−4xydydx+8y2=0 का हल है |
View Solutionयदि एक वक्र y=f(x) बिन्दु (1,−1) से होकर जाता है तथा अवकल समीकरण y(1+xy)dx=xdy को संतुष्ट करता है, तो f(−12) बराबर है-
View Solutionवक्र y=c1ec2x को निरूपित करने वाला अवकल समीकरण है:
View Solutionमाना a,b,c वास्तविक संख्याएं है, a≠0 यदि समीकरण a2x2+bx+c=0 का मूल α है तथा समीकरण a2x2−bx−c=0 का मूल β है तथा 0<α<β तो समीकरण a2x2+2bx+2c=0 का एक मूल γ किस प्रतिबन्ध को संतुष्ट करेगा?
View Solution
