बिंदु (−5,13) से होकर जाने वाली दो सरल रेखाओ के समीकरण दीजिए|इस प्रकार की कितनी रेखायें सम्भव है?
माना रेखा का समीकरण निम्न है
ax+by=c ...(1)
यह बिंदु (−5,13) से होकर जाती है|
∴ a(−5)+b(13)=c ltbr gt ⇒ −5a+13b=c
अब a और b के कोई भी मान लेकर c का मान ज्ञात करते है| ...(2)
माना a=0 और b =1 ⇒ c=13
a ,b और c के यह मान समी (1 ) में रखने पर
0⋅x+1⋅y=13 ⇒ y=13
माना a=4,b=2 ⇒ c=6 [(2 ) से ]
a,b और c के यह मान समी (1 )में रखने पर
4x+2y=6 ⇒ 2x+y=13
इस प्रकार हम बहुत-सी समीकरण प्राप्तं कर सकते है|
अतः (-5 ,13 ) से होकर जाने वाली अनंत रेखाएं हो सकती है|
Topper's Solved these Questions
- दो चरों वाले रैखिक समीकरण BOOK - NOOTAN HINDICHAPTER - दो चरों वाले रैखिक समीकरण EXERCISE - प्रश्नावली
8 Videos
- दो चरों वाले रैखिक समीकरण BOOK - NOOTAN HINDICHAPTER - दो चरों वाले रैखिक समीकरण EXERCISE - प्रश्नावली 4.1
2 Videos
- त्रिभुज BOOK - NOOTAN HINDICHAPTER - त्रिभुज EXERCISE - विविधि प्रश्नावली ( दीर्घ उत्तरीय प्रश्न )
8 Videos
- निर्देशांक ज्यामिति BOOK - NOOTAN HINDICHAPTER - निर्देशांक ज्यामिति EXERCISE - विविध प्रश्नावली
8 Videos
Similar Questions
निम्नलिखित प्रत्येक समीकरण का आलेख बनाइए:
(i) x=4 (ii)x−6=0 (iii)x+3=0 (iv)y=2 (v)2x−5=0 (vi)y+3=0
View Solutionएक नोटबुक की कीमत एक कलम की कीमत से दोगुनी है| इस कथन को निरूपित करने के लिए दो चरो वाला एक रैखिक समीकरण लिखिय|
[संकेत: मान लीजिए,नोटबुक की कीमत रु x है और कलम की कीमत रु y है]
View Solutionदी आकृति में, यदि x = y और AB = CB है, तो सिद्ध कीजिए कि AE = CD है।
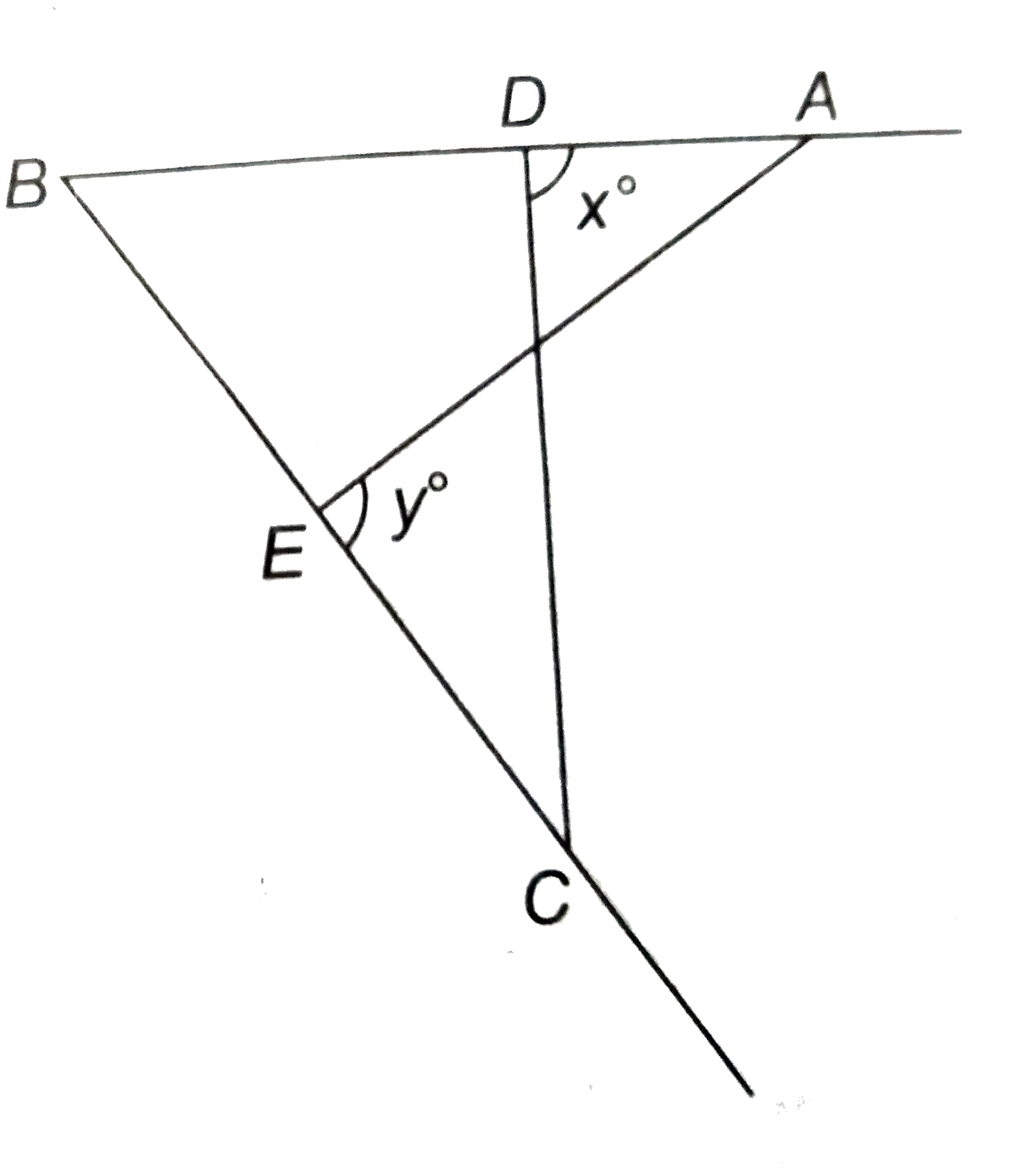
View Solutionमूल बिन्दु के निर्देशांक लिखिए |
View Solutionबिंदु (3,−5) से जाने वाली तथा दोनों अक्षो से बराबर किन्तु विपरीत चिन्हो के अन्तः खण्ड काटने वाली सरल रेखा का समीकरण ज्ञात कीजिए
View Solutionकिसी वर्ग के विपरीत शीर्षो के निर्देशांक (1,2) तथा (3,8) है , तो शीर्ष (1,2) से होकर जाने वाली रेखाओ तथा विकर्ण का समीकरण ज्ञात कीजिए ।
View Solutionउस सरल रेखा का समीकरण ज्ञात कीजिए जो रेखा 7x−5y+14=0 के समान्तर है तथा रेखाओ 2x+3y+7=0 और 3x−4y−15=0 के प्रतिच्छेद बिंदु से होकर जाती है ।
View Solutionदो बिंदु (1,3) और(0,4) इस प्रकार है की एक गतिमान बिंदु से बने त्रिभुज का क्षेत्रफल सदैव 25 वर्ग इकाई रहता है । उस बिंदु के बिन्दुपथ का समीकरण ज्ञात कीजिए
View Solutionसरल रेखा x+22=2y−76=5−z6 की दिक्- कोज्याएं ज्ञात कीजिए । साथ ही बिंदु A(−1,2,3) से होकर जाने वाली तथा दी हुई रेखा के समांतर रेखा का सदिश समीकरण ज्ञात कीजिए।
View Solutionउन दो सरल रेखाओं के समीकरण ज्ञात कीजिए जो बिन्दु (0,a) से होकर जाती है तथा जिन पर बिन्दु (2a,2a) से खींचे गए लम्बो की माप a है।
View Solutionबिंदु (1,2,3) से गुजरने वाली तथा दिक् अनुपात 4,5,6 वाली सरल रेखा का समीकरण ज्ञात कीजिए।
View Solutionबिंदु (1,2,3) से होकर जाने वाली रेखा का समीकरण ज्ञात कीजिए जो रेखा x−y+2z=5,3x+y+z=6 के समान्तर है।
View Solutionबिंदु (3,1,−6) से होकर जाने वाली रेखा का समीकरण ज्ञात कीजिए जो रेखा x+y+2z−4=0,2x−3y+z+5=0 के समान्तर है।
View Solutionबिंदु (0,0,0) से होकर जाने वाली रेखा का समीकरण ज्ञात कीजिए जो रेखा x+y+z+2=0,4x+3y+2z+1=0 के समान्तर है।
View Solutionबिंदु (2,3,5) से होकर जाने वाली रेखा का समीकरण ज्ञात कीजिए जो रेखा x+2y−2z=7,6x+8y−9z=1 के समान्तर है।
View Solutionवृत्त के बाहर स्थित बिंदु से खींची गई स्पर्श रेखाओं की संख्या हो सकती है:
View Solution
