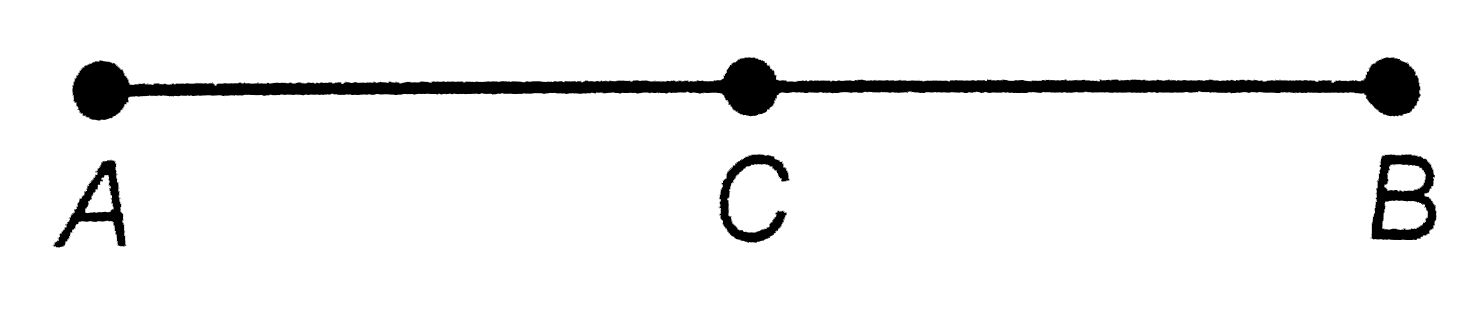
यदि दो बिन्दुओं A और B के बीच एक विन्दु होता C ऐसा स्थित है कि AC=BC है, तो सिद्ध कीजिए कि है एक आकृति खींच कर इसे स्यष्ट कीजिए।
यहाँ AC=BC, दोनों पक्षों में AC जोड़ने पर, AC+AC=BC+AC (यदि बारबारो को बारबारो में जोड़ा जाए तो पूर्ण भी बराबर होते है)
Topper's Solved these Questions
- यूक्लिड की ज्यामिति का परिचय BOOK - NOOTAN HINDICHAPTER - यूक्लिड की ज्यामिति का परिचय EXERCISE - प्रश्नावली
30 Videos
- प्रायिकता BOOK - NOOTAN HINDICHAPTER - प्रायिकता EXERCISE - विविध प्रश्नावली ( अतिलघु उत्तरीय/ लघु उत्तरीय प्रश्न)
10 Videos
- रचनाएँBOOK - NOOTAN HINDICHAPTER - रचनाएँEXERCISE - विविध प्रश्नावली
7 Videos
Similar Questions
बताइए कि निम्नलिखित में से कौन-से सत्य और कौन-से असत्य हैं?
प्रत्येक किरण की परिमित लम्बाई होती है।
View Solutionएक असम्भव घटना की प्रायिकता क्या है ?
View Solutionनिम्नलिखित कोणो को बनाइए:
(i) 60∘ (ii)90∘ (iii) 120∘ (iv) 180∘ (v) 270∘
View Solutionसिद्ध कीजिए कि समीकरण y2+2ax+2by+c=0 एक परवलय निरूपित करती है जिसका अक्ष x-अक्ष के समान्तर है । इसका शीर्ष ज्ञात कीजिए ।
View Solutionसिद्ध कीजिए कि बिंदु (1,−6),(5,2),(7,0) तथा (−1,−4)एक चक्रीय चतर्भुज के शीर्ष है ।
View Solutionसिद्ध कीजिए कि ΔABC एक समद्विबाहु त्रिभुज है यदि
∣∣ ∣ ∣∣1111+cosA1+cosB1+cosCcos2A+cosAcos2B+cosBcos2C+cosC∣∣ ∣ ∣∣=0
View Solutionमाना कि N में एक द्वि - आधारी संकिया ∗, a∗b=a तथा b के LCM द्वारा परिभाषित है , a,b∈N तब सिद्ध कीजिए कि :(20∗16)∗8=20∗(16∗8)
View Solutionएक ही आधार BC पर तीन समद्विबाहु त्रिभुज △PBC ,△QBC और △RBC स्तिथ है। सिद्ध कीजिए कि P ,Q और R समरेख है।
View Solutionयदि ¯¯¯¯¯¯OA=¯a,¯¯¯¯¯¯OB=¯b तथा C,AB पर एक ऐसा बिंदु है कि ¯¯¯¯¯¯AC=3¯¯¯¯¯¯AB तो सदिश ¯¯¯¯¯¯OC बराबर है:
View Solutionयदि ¯a,¯b दो सदिश इस प्रकार है कि ∣∣¯a+¯b∣∣=|¯a|, तो सिद्ध कीजिए कि 2¯a+¯b सदिश ¯b पर लम्ब है |
View Solutionयदि दो सदिश ¯a और ¯b इस प्रकार हैं कि ∣∣¯a+¯b∣∣=∣∣¯b∣∣, तब सिद्ध कीजिए कि ¯a+2¯b, सदिश ¯a पर लम्ब है |
View Solutionयदि बिन्दु (a,b),(a',b') और (a−a',b−b') संरेख हो तो सिद्ध कीजिए कि
ab'=a'b.
साथ ही यह भी सिद्ध कीजिए कि इन बिन्दुओं से होकर जाने वाली रेखा मुलबिन्दु से होकर जाती है।
View Solutionसिद्ध कीजिए कि बिन्दु (2,−2),(8,4),(5,7) और (−1,1) एक आयत के शीर्ष है। उसके विकर्णों के बीच का न्यून कोण ज्ञात कीजिए।
View Solutionयदि f:R→R इस प्रकार है कि f(x) = |x|, तो सिद्ध कीजिए कि fof = f .
View Solutionसारणिक के गुणों का प्रयोग करके सिद्ध कीजिए कि ∣∣ ∣ ∣∣−bcb2+bcc2+bca2+ac−acc2+aca2+abb2+ab−ab∣∣ ∣ ∣∣=(ab+bc+ac)3
View Solutionयदि →a×→b=→c×→bतो सिद्ध कीजिए →a−→c=λ→b कि जहाँ एक λ अदिश है।
View Solution
