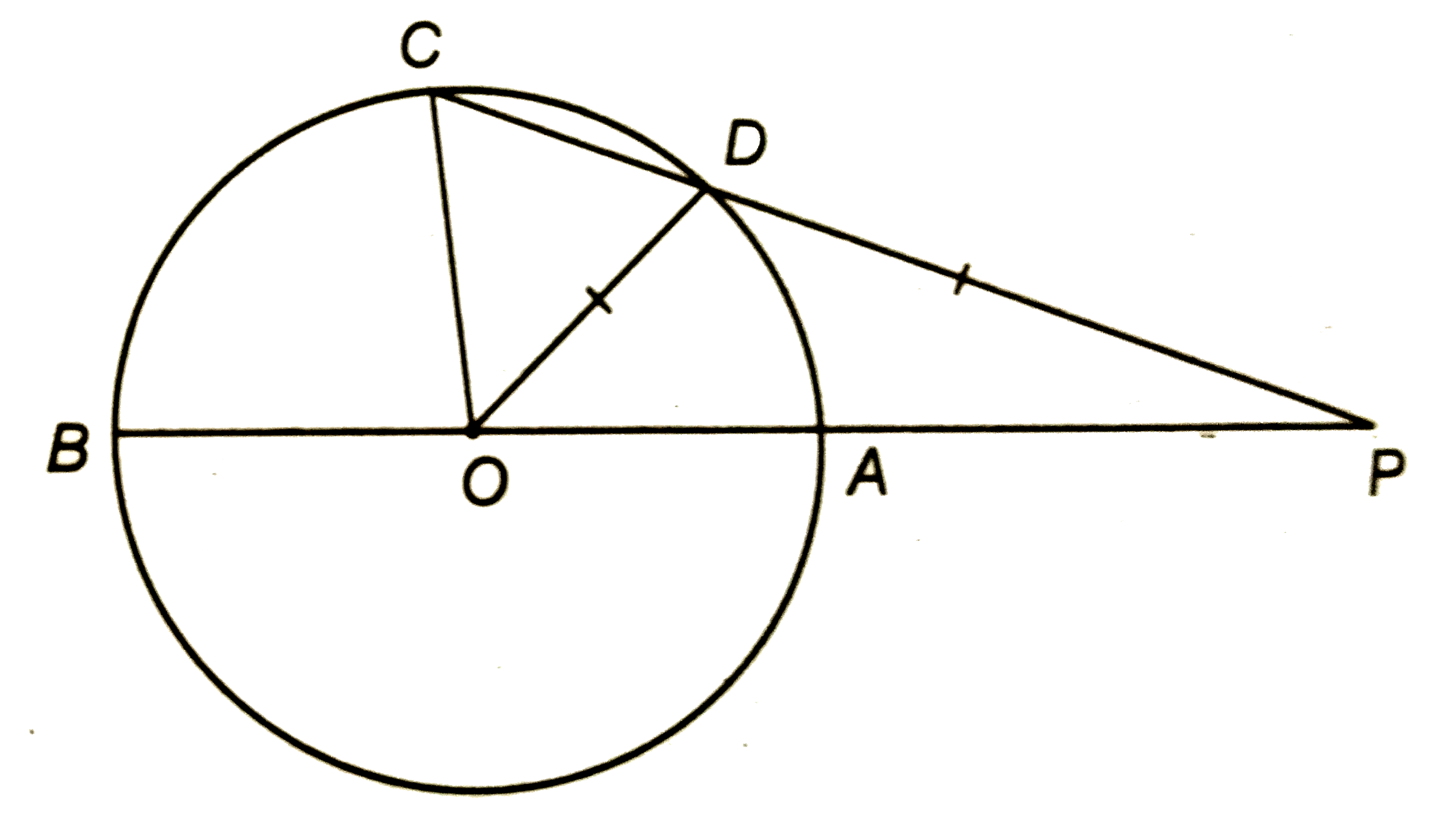
O' केन्द्र के वृत्त के बाहर एक बिन्दु P स्थित है | P से वृत्त पर दो रेखाएँ PAOB और PDC खींची गयी हैं | यदि PD = DO, तो सिद्ध कीजिए कि चाप BC=3× चाप AD.
ΔDOP में,
DO=DP
⇒ ∠DPO=∠DOP
माना ∠DPO=∠DOP=x
अब ΔODP में,
∠ODC बहिष्कोण है |
∴ ∠ODC=∠DOP+∠DPO
=x+x
=2x
ΔOCD में,
OC=OD (वृत्त की त्रिज्याएँ हैं)
⇒ ∠ODC=∠OCD=2x
∴ ∠COD=180∘−∠ODC−∠OCD
=180∘−2x−2x
=180∘−4x
अब ∠BOC+∠COD+∠DOP=180∘
⇒ ∠BOC+180∘−4x+x=180∘
⇒ ∠BOC=3x
∴ ∠BOC∠DOP=3xx
⇒ ∠BOC∠DOA=3
⇒ चाप BCचाप AD=3
⇒ चाप BC=3× चाप AD
Topper's Solved these Questions
- वृत्त BOOK - NOOTAN HINDICHAPTER - वृत्त EXERCISE - प्रश्नावली 10A
21 Videos
- वृत्त BOOK - NOOTAN HINDICHAPTER - वृत्त EXERCISE - प्रश्नावली 10B
19 Videos
- रेखाएं और कोण BOOK - NOOTAN HINDICHAPTER - रेखाएं और कोण EXERCISE - दीर्घ उत्तरीय प्रशन
5 Videos
- संख्या पद्धतिBOOK - NOOTAN HINDICHAPTER - संख्या पद्धतिEXERCISE - विविध प्रश्नावली (लघु उत्तरीय प्रश्न)
10 Videos
Similar Questions
एक वृत्त में 10 सेमी लम्बी जीवा केन्द्र से 12 सेमी कि दूरी पर है | इसी वृत्त के केन्द्र से 5 सेमी की दूरी पर स्थित जीवा की लम्बाई क्या होगी ?
View Solutionसंलग्न चित्र में, 'O' वृत्त का केन्द्र है | यदि ∠ACB=25∘, तो ∠AOB ज्ञात कीजिए |

View SolutionΔABC की भुजा BC को D तक बढ़ाया जाता है ∠A का समद्विभाजक BC को L पर मिलता है ।
सिद्ध कीजिये कि ∠ABC+∠ACD=2∠ALC
View Solution−14 और 25 के मध्य दो परिमेय संख्याएँ ज्ञात कीजिए ।
View Solutionवृत्त के बाहर स्थित बिंदु से खींची गई स्पर्श रेखाओं की संख्या हो सकती है:
View Solutionएक वृत्त X-अक्ष पर एक जीवा काटता है जिसकी लम्बाई 4a है तथा यह वृत्त Y-अक्ष के एक बिन्दु से होकर जाता है जिसकी मूलबिंदु से दुरी 2b है , तो वृत्त के केन्द्र का बिन्दुपथ (locus) है
View Solutionखण्ड 'अ'खण्ड 'ब'1.वृत्त के अन्तः बिंदु से खींची गयी स्पर्श रेखाओं की संख्या(a)समकोण2.वृत्त के किसी बिंदु से खींची गयी स्पर्श रेखाओं की संख्या(b)स्पर्श रेखा3.वृत्त के बाह्य बिंदु से वृत्त पर खींची गयी स्पर्श रेखाओं की संख्या(c)शून्य4.स्पर्श रेखा और स्पर्श बिंदु से जाने वाली त्रिज्या के बीच बना कोण(d)एक5.वृत्त को केवल एक बिंदु पर प्रतिच्छेद करने वाली रेखा(e)दो
View Solutionकिसी वृत्त में एक चाप केन्द्र पर 45∘का कोण बनाता है। यदि चाप की लम्बाई 11 सेमी है तो वृत्त की त्रिज्या ज्ञात कीजिए।
View Solutionयदि किसी वृत्त के व्यास का एक सिरा (3,4) और केन्द्र (2,3) हो, तो दूसरे सिरे के निर्देशांक ज्ञात कीजिए।
View Solutionयदि कोई जीवा वृत्त के केन्द्र से गुजरती है, तो उसे ........." कहते हैं।
View Solutionएक वृत्त के चाप द्वारा अंतरित कोण|प्रमेय 10.8#!#उदाहरण
View Solutionवृत्त|वृत्त के चाप द्वारा आन्तरित कोण#!#महत्वपूर्ण प्रश्न
View SolutionPA and PB are tangents to a circle with centre O, from a point P outside the circle, and A and B are points on the circle. If angle APB= 40^@ , then angle OAB is equal to: PA तथा PB एक वृत्त के बाहर स्थित बिंदु P से वृत्त की स्पर्श रेखाएं हैं जिसका केंद्र O है तथा A और B वृत्त पर स्थित बिंदु हैं | यदि angle APB= 40^@ है, तो angle OAB का मान ज्ञात करें |
View SolutionPA and PB are two tangents from a point P outside a circle with centre O. If A and B are points on the circle such that angle APB= 80^@ , then angle OAB is equal to: PA और PB केंद्र O वाले वृत्त के बाहर स्थित बिंदु P से निकली दो स्पर्श रेखाएं हैं | यदि A और B वृत्त पर स्थित ऐसे दो बिंदु हैं कि angle APB= 80^@ है, तो angle OAB का मान क्या होगा ?
View SolutionPA and PB are the tangents to a circle with centre O, from a point P outside the circle. A and B are the points on the circle. If angle APB= 72^@ ,then angle OAB is equal to: PA तथा PB एक वृत्त पर वृत्त के बाहर स्थित बिंदु P से खींची गयी स्पर्श रेखाएं हैं जिसका केंद्र O है | A तथा B वृत्त पर स्थित बिंदु हैं | यदि angle APB= 72^@ है, तो angle OAB का मान ज्ञात करें |
View Solution
