चक्रीय चतुर्भुज ABCD के विकर्ण AC और BD एक दूसरे को E पर समकोण पर प्रतिच्छेद करते हैं (चित्र देखें) | E से होकर जाने वाली तथा AB के लम्बवत रेखा l, CD को F पर मिलती है | सिद्ध कीजिए कि F, CD का मध्य बिन्दु है |
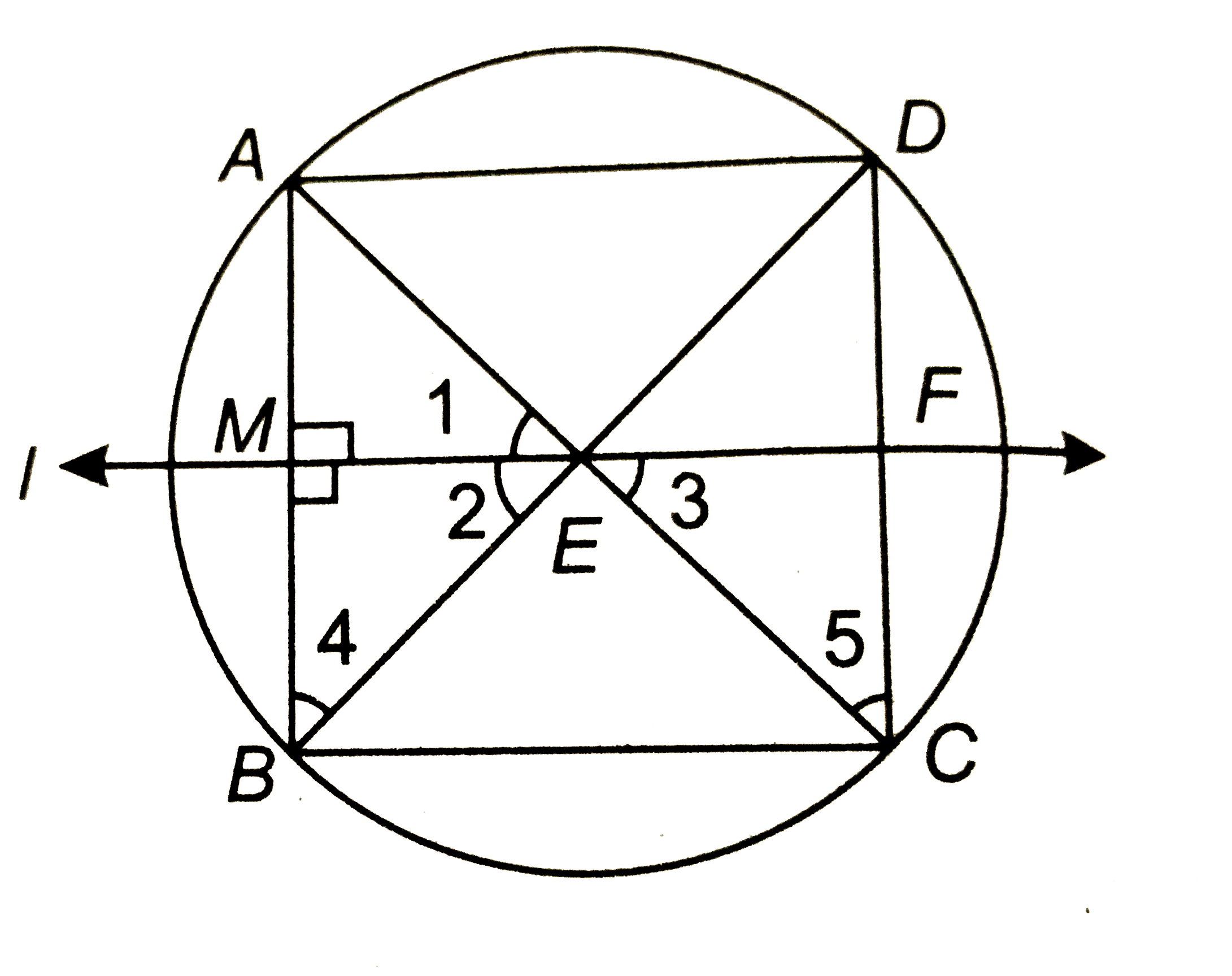
ABCD एक चक्रीय चतुर्भुज है जिसमें विकर्ण AC और BD समकोण पर बिन्दु E पर प्रतिच्छेद करते हैं | E से होकर जाने वाली और AB के लम्बवत रेखा l, CD को F पर मिलती है |
यहाँ ∠AEB=90∘ (∵ विकर्ण समकोण पर काटते हैं)
⇒ ∠1+∠2=90∘
⇒ ∠=90∘−∠2 ...(1)
पुन: ∠EMB=90∘ (∵EM⊥AB)
ΔEMB में,
∠2+∠4=90∘
⇒ ∠4=90∘−∠2 ...(2)
समीकरण (1) और (2) से,
∠1=∠4
लेकिन ∠1=∠3 (शीर्षाभिमुख कोण)
∴ ∠3=∠4
तथा, ∠4=∠5 (एक वृत्तखण्ड के कोण बराबर होते हैं)
⇒ ∠3=∠5
⇒ CF=EF (त्रिभुज में समान कोणों कि सम्मुख भुजाएँ बराबर होती हैं)
इसी प्रकार, DG=EF
⇒ CF=DF
अत: F, CD का मध्य बिन्दु है |
Topper's Solved these Questions
- वृत्त BOOK - NOOTAN HINDICHAPTER - वृत्त EXERCISE - प्रश्नावली 10A
21 Videos
- वृत्त BOOK - NOOTAN HINDICHAPTER - वृत्त EXERCISE - प्रश्नावली 10B
19 Videos
- रेखाएं और कोण BOOK - NOOTAN HINDICHAPTER - रेखाएं और कोण EXERCISE - दीर्घ उत्तरीय प्रशन
5 Videos
- संख्या पद्धतिBOOK - NOOTAN HINDICHAPTER - संख्या पद्धतिEXERCISE - विविध प्रश्नावली (लघु उत्तरीय प्रश्न)
10 Videos
Similar Questions
एक वृत्त में 10 सेमी लम्बी जीवा केन्द्र से 12 सेमी कि दूरी पर है | इसी वृत्त के केन्द्र से 5 सेमी की दूरी पर स्थित जीवा की लम्बाई क्या होगी ?
View Solutionसंलग्न चित्र में, 'O' वृत्त का केन्द्र है | यदि ∠ACB=25∘, तो ∠AOB ज्ञात कीजिए |

View SolutionΔABC की भुजा BC को D तक बढ़ाया जाता है ∠A का समद्विभाजक BC को L पर मिलता है ।
सिद्ध कीजिये कि ∠ABC+∠ACD=2∠ALC
View Solution−14 और 25 के मध्य दो परिमेय संख्याएँ ज्ञात कीजिए ।
View SolutionIn the figure above (not to scale), ¯¯¯¯¯¯AB⊥¯¯¯¯¯¯CDandAD is the bisector of ∠BAE.AB=3cm and AC=5cm. Find CD.
View SolutionMatch the following Column A to Column B

View SolutionIn the figure (not to scale) AB = AC and BD = CD. Find ∠ADB
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/PS_MATH_IX_C15_E05_003_Q01.png" width="80%"gt
View Solutionबिन्दु (1,0,0) से जाने वाली उस रेखा का समीकरण ज्ञात कीजिए जो XZ-समतल पर लम्ब है।
View Solutionबिंदु A(−2,−4)से होकर जाने वाली रेखा X-अक्ष के साथ45∘ का कोण बनाती है तथा रेखा x+3y=8 को बिंदु P पर काटती है AP, के बीच कि दूरी ज्ञात कीजिए ।
View Solutionएक रेखा X- अक्ष तथा Y-अक्ष को बिंदु A तथा B पर मिलती है AB का मध्य बिंदु (x1,y1) है तो रेखा का समीकरण है -
View Solutionयदि बिन्दु (a,b),(a',b') और (a−a',b−b') संरेख हो तो सिद्ध कीजिए कि
ab'=a'b.
साथ ही यह भी सिद्ध कीजिए कि इन बिन्दुओं से होकर जाने वाली रेखा मुलबिन्दु से होकर जाती है।
View Solutionसिद्ध कीजिए कि एक पासो के जोड़े को फेंकने पर पहले पर 5 आना , दूसरे पास पर 6 आने कि स्वतन्त्र घटनाएँ है।
View Solutionएक अतिपरवलय बिन्दु P(√2,√3) से होकर जाता है, तथा उसकी नाभियाँ (±2,0) पर है, तो अतिपरवलय के बिन्दु P पर खींची गई स्पर्श रेखा जिस बिन्दु से होकर जाती है, वह है
View Solutionएक त्रिभुज का एक शीर्ष (1,2) पर है तथा इससे होकर जाने वाली दो भुजाओं के मध्य - बिन्दु (−1,1) और (2,3) हैं , तो इस त्रिभुज का केन्द्रक है
View Solutionसरल रेखा x+2y=1 निर्देशांक अक्षों को A तथा B पर काटती है। मूलबिंदु , A तथा B से होकर जाने वाला वृत्त खींचा गया है , तो मूलबिंदु पर वृत्त की स्पर्श रेखा की A तथा B से लम्बवत दूरियों का योग है
View Solutionयदि एक वक्र बिंदु (1, -2) से होकर जाता है तथा इस पर किसी बिंदु (x, y) पर स्पर्श रेखा का ढाल (slope) x2−2yx है, तो यह वक्र निम्न में से किस बिंदु से होकर जाता है ?
View Solution
