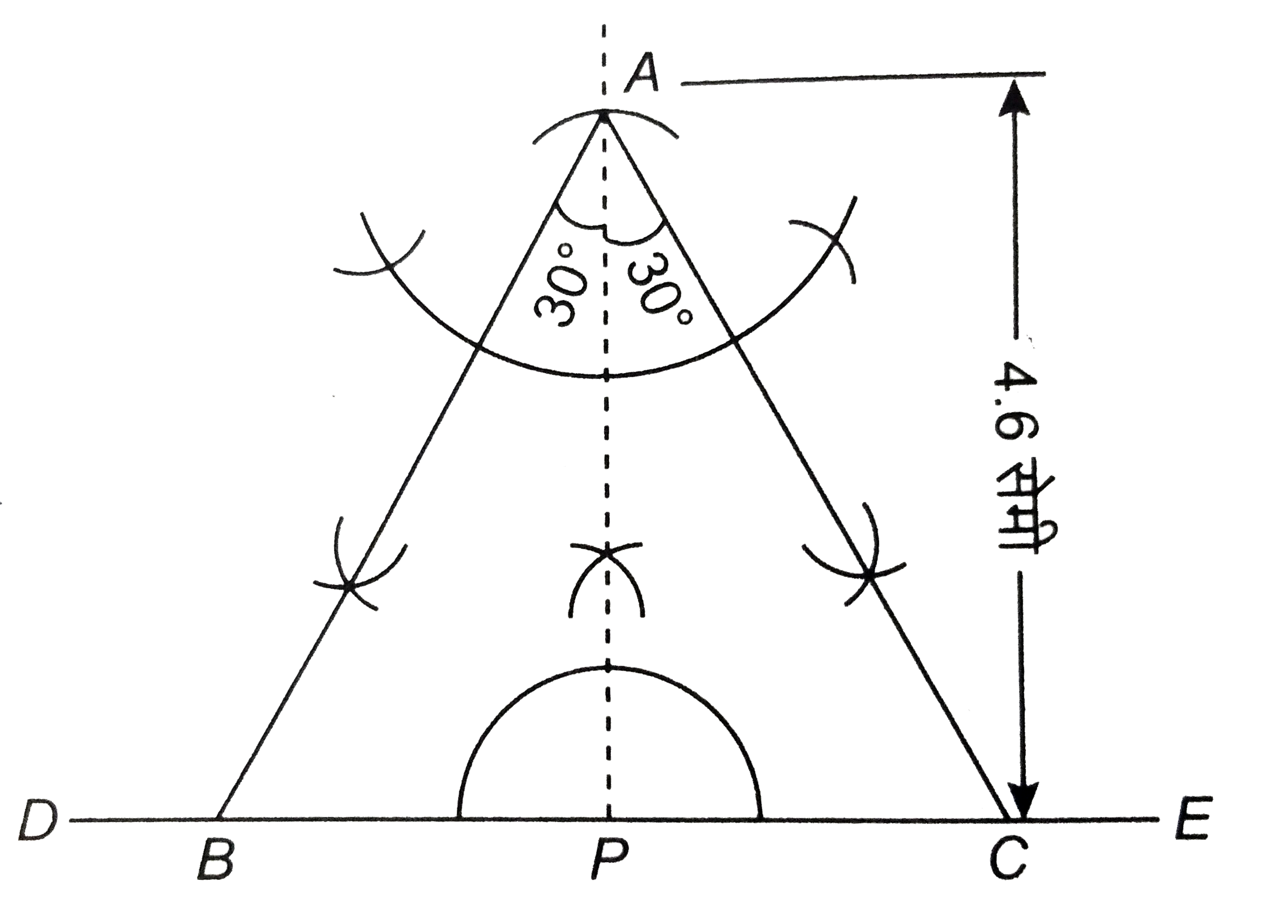
एक समद्विवाहु त्रिभुज की रचना कीजिए जिसका शीर्ष कोण 60∘शीर्ष लंब 4.6 है।
रचना के चरण:
1 एक रेखा DE खीचकर इस पर एक बिन्दु P हैं।
2. ∠APE=90∘ बनाते हैं और PA=4.6 सेमी काटते है
∠CAP=∠BAP=12×60∘=30∘ खीवते है, जो DE को क्रमशः C और B पर मिलते हैं।
△ABC अभीष्ट त्रिभुज है।
Topper's Solved these Questions
- रचनाएँBOOK - NOOTAN HINDICHAPTER - रचनाएँEXERCISE - प्रश्नावली
13 Videos
- रचनाएँBOOK - NOOTAN HINDICHAPTER - रचनाएँEXERCISE - प्रश्नावली 11.1
7 Videos
- यूक्लिड की ज्यामिति का परिचय BOOK - NOOTAN HINDICHAPTER - यूक्लिड की ज्यामिति का परिचय EXERCISE - प्रश्नावली
30 Videos
- रेखाएं और कोण BOOK - NOOTAN HINDICHAPTER - रेखाएं और कोण EXERCISE - दीर्घ उत्तरीय प्रशन
5 Videos
Similar Questions
निम्नलिखित कोणों की रचना कीजिए:
(i) 60∘ (ii) 30∘ (iii) 15∘
View Solutionएक दी हुई किरण के प्रारम्भिक बिन्दु पर 90∘ के कोण की रचना कीजिए और कारण सहित रचना की पुष्टि कीजिए।
View Solutionबताइए कि निम्नलिखित में से कौन-से सत्य और कौन-से असत्य हैं?
प्रत्येक किरण की परिमित लम्बाई होती है।
View SolutionΔABC की भुजा BC को D तक बढ़ाया जाता है ∠A का समद्विभाजक BC को L पर मिलता है ।
सिद्ध कीजिये कि ∠ABC+∠ACD=2∠ALC
View Solutionसिद्ध कीजिए कि समीकरण y2+2ax+2by+c=0 एक परवलय निरूपित करती है जिसका अक्ष x-अक्ष के समान्तर है । इसका शीर्ष ज्ञात कीजिए ।
View Solutionसिद्ध कीजिये की बिंदु (1,−2),(3,6),(5,10) और (3,2) एक समांतर चतुर्भुज के शीर्ष है ।
View Solutionएक समकोण समद्विबाहु त्रिभुज के कर्ण का समीकरण 3x+4y=4 है । यदि इसके सम्मुख शीर्ष के निर्देशांक (2,2)है , तो त्रिभुज की शेष दो भुजाओ के समीकरण ज्ञात कीजिए ।
View Solutionकिसी समबाहु त्रिभुज के आधार का समीकरण x+y=2 है तथा सामने के शीर्ष के निर्देशांक (2,1) है , त्रिभुज की शेष भुजाओ के समीकरण ज्ञात कीजिए ।
View Solutionमाना A(2,−3) तथा B(−2,1) एक त्रिभुज ABC के शीर्ष है । यदि इस त्रिभुज का केन्द्रक सरल रेखा 2x+3y=1पर भ्रमण करता है तो शीर्ष C का बिन्दुपथ है -
View Solutionएक परवलय की नाभि मूलबिंदु पर है तथा रेखा x=2 परवलय की नियता है , तो परवलय का शीर्ष है
View Solutionत्रिभुज ABC की मध्याकाओं की लम्बाई ज्ञात कीजिए, जिसके शीर्ष A(3, -2), B(0, 6) और C(-2, 4) है ।
View Solutionवह त्रिभुज जिसका लांबकेंद्र त्रिभुज का शीर्ष बिंदु होता है ,कहलाता है -
View Solutionएक त्रिभुज , जिसके शीर्ष (0,0),(0,41) तथा (41,0) है , के आंतरिक भाग में स्थित उन बिंदुओं की संख्या जिनके दोनों निर्देशांक पूर्णांक है , है :
View Solutionकिसी त्रिभुज के शीर्ष बिन्दुओं के निर्देशांक (0,1),(2,0) और (-1,-2) है। उसकी भुजाओं के समीकरण ज्ञात कीजिए।
View Solutionसिद्ध कीजिए कि बिन्दु (2,−2),(8,4),(5,7) और (−1,1) एक आयत के शीर्ष है। उसके विकर्णों के बीच का न्यून कोण ज्ञात कीजिए।
View Solutionमान A(2,−3) तथा B(−2,1) एक त्रिभुज ABC के शीर्ष है। यदि इस त्रिभुज का केन्द्रक सरल रेखा 2x+3y=1 पर भ्रमण करता है, तो शीर्ष C का बिन्दुपथ है:
View Solution
