Four equal circles are described about the four corners of a square so that each touches two of the others. The shaded area enclosed between the circles 247cm2, find the radius of the circle.
Let the radius of the circle be R
area of 4 sets=π⋅R24⋅4=π⋅R2
area of square=(2R)2=4R2
area of shaded region =247
4R2−πR2=247
R2(4−227)=247
R228−227=27
R2⋅6=24
R=√4=2cm
সম্পর্কিত প্রশ্ন
In the given figure, four equal circles are described about corners of a square so that each circle touches two of the circles as shown in the figure. Find the area of the shaded region, each side of the square measuring 14 cm.
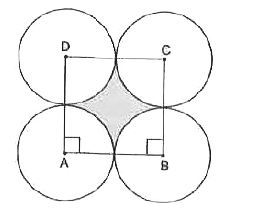
View SolutionFour equal circles are described about the four corners of a square so that each touches two of the others as shown in Fig. 15.38. Find the area of the shaded region, each side of the square measuring 14 cm. (FIGURE)
View Solutionकिसी वर्ग के चारों कोनों पर चार बराबर त्रिज्या वाले वृत्त इस प्रकार खींचे है कि प्रत्येक वृत्त दूसरे दो वृत्तों को स्पर्श करता है । यदि वर्ग की प्रत्येक भुजा 140 सेमी. हो तो वृत्त की परिधि के बीच परिबद्ध स्थान का क्षेत्रफल बताइए? यह मानते हुए कि π=227
View SolutionFour circles of equal radii are described about the four corners of a square so that each touches two of the other circles. If each side of the square is 140 cm then area of the space enclosed between the circumference of the circle is (taken π=22/7 )
View Solutionयदि 3cm त्रिज्या के चार समान वृत्त परस्पर बाह्य स्पर्श करते है तदनुसार चार वृत्तों से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिये ?
View SolutionFour equal circles are described about the four corners of a square so that each circle touches two of the others. Find the area of the space enclosed between the circumferences of the circles, each side of the square mea suring 24 cm.
View Solutionकिसी वर्ग के चारो कोनो पर 4 सेमी त्रिज्या के चार बराबर वृत्त एक-दूसरे को बाह्य स्पर्श करते है। छायाकिंत भाग की क्षेत्रफल क्या होगा?
View SolutionThe four equal circles of radius 4 cm drawn of the four corners of a square touch each other externally. Then the area of the portion between the square and the four sectors is
View Solution
