A sample of 0.177g of an ideal gas occupies 1000cm3at STP. Caculate the rms speed of gas molecules.
Vr.m.s.=√3ρ√ρ
Here P=105Pa=1atm
=√3×105×10−3√1.77×10−4
=1301.8=1302ms.
Topper's Solved these Questions
- KINETIC THEORY OF GASESBOOK - HC VERMACHAPTER - KINETIC THEORY OF GASESEXERCISE - Objective 2
7 Videos
- INTRODUCTION TO PHYSICSBOOK - HC VERMACHAPTER - INTRODUCTION TO PHYSICSEXERCISE - Exercises
19 Videos
- LAWS OF THERMODYNAMICSBOOK - HC VERMACHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Short Answer
15 Videos
Similar Questions
Knowledge Check
The rms speed of a gas molecule is
A√M3RTBM3RTC√3RTMD(3RTM)20.28 g of a gas occupies 227 ml at STP. The gas could be:
AN2BCOCC2H4DN2O40.28 g of a gas occupies 227 mL at STP. The gas could be:
AN2BCOCC2H4DN2O4
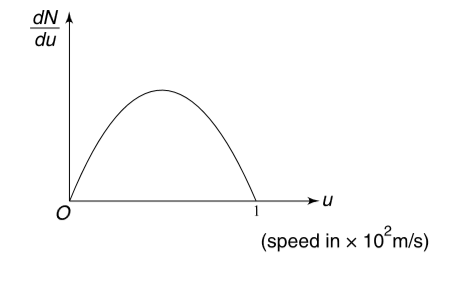
The speed distribution of molecules in a sample of a gas is shown in the figure. The graph between dNdu and u is a parabola and total number of molecules in the sample is N0.
(a) Calculate the rms speed of the molecules.
(b) Calculate the total translational kinetic energy of molecules if mass of the sample is 10 g.
View SolutionSuppose a gas sample in all have 6×1023 molecules Each 1/3rd of the molecules have rms speed 104cm/sec,2×104cm/sec and 3×104cm/sec Calculate the rms speed of gas molecules in sample .
View SolutionA fiven sample of an ideal gas occupise a volume V at a pressure p and sbsoulte temperature T.The mass of each molecule of the gas is m. Which of the following fives the dinsity of the gas ?
View SolutionThe temperature of an ideal gas is increased from 27∘C to 927∘C. The rms speed of its molecules becomes.
View SolutionA sample of an ideal gas occupies a volume V at pressure P and absolute temperature T. The mass of each molecule is m, then the density of the gas is
View Solution
