The human body has an average temperature of 98∘F.Assume that vapour pressure of the blood in the veins beahaves like that of pure water. Find the minimum atmosphric pressure which is necessary to prevent the blood from boling. Use figure of the text for the vapour.
The temperature of body is 98∘F=37∘C .
At37∘Cfrom the graph SVP = just less
than 50 mm
B.P. is the temperature when atmospheric
pressure equal the vapour pressure of the
blood. Thus minimum, pressure to prevent
boiling is 50 mm of Hg.
Topper's Solved these Questions
- KINETIC THEORY OF GASESBOOK - HC VERMACHAPTER - KINETIC THEORY OF GASESEXERCISE - Objective 2
7 Videos
- INTRODUCTION TO PHYSICSBOOK - HC VERMACHAPTER - INTRODUCTION TO PHYSICSEXERCISE - Exercises
19 Videos
- LAWS OF THERMODYNAMICSBOOK - HC VERMACHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Short Answer
15 Videos
Similar Questions
A lake filled with water has depth H, A pipe of length slightly less than H lies at the bottom of the lake. It contains an ideal gas filled up to a length of H10 A smooth an ideal gas filled up to a length gas in place. Now the pipe is slowly raised to vertical position (see figure). Assume that temperature of the gas remains Constant and neglect the atmospheric pressure.
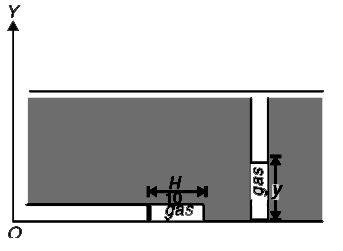
(a) Plot the variation of pressure inside the lake as a function of height y from the base. Let the height of piston frm the base, after the pipe is made vertical, by y. plot the variation of gas pressure as a function of y in the first graph itself.
(b) In equilibrium the gas pressure and the pressure due to water on the piston must be equal. Using this solve for equilibrium height y0 of the piston. You get two answers. Which one is correct and why?
View SolutionA helium balloon has its rubber envelope of weight wRubber and its is used to lift a weight of wLoad. The volume of fully inflated balloon is V0. The atmospheric temperature is T0 throughout and the atmospheric pressure is known to change with height y according to equation P=P0e–ky where k is a positive constant and P0 is atmospheric pres- sure at ground level. The balloon is inflated with sufficient amount of helium so that the net upward force on is F0 at the ground level. Assume that pressure inside the balloon is always equal to the outside atmospheric pressure. Density of air and helium at ground level is ρa and ρHe respectively.
(a) Find the number of moles (n) of the helium in the balloon.
For following two questions assume n to be a known quantity.
(b) Find the height (y(0)) at which the balloon is fully inflated.
(c) Prove that the balloon will be able to rise to height y0 if nRT0gP0(ρa−ρHg)>wRubber+wLoad
View Solution
Knowledge Check
When we add a non-volatile solute to a solvent lowers its vapour pressure. Therefore, the vapour pressure of a solution is lower than that of pure solvent, at the same temperature. A higher temperature is needed to raise the vapour pressure upto one atmosphere pressure, when boiling point is attained. However, b.pt. increases small. For example, 0.1 molal aqueous sucrose solution boils at 100.05∘C. Sea water, which is rich in Na+ and Cl− ions, freezes about 1∘C lower than freezes pure water. At the freezing point of a pure-solvent, the rates at which two molecule stick together to form the solute is present. Few solvent molecules are in constant with surface of solid. However, the rate at which the solvent molecules leave the surface of solid remains unchanged. That is why temperature is lowered to restore the equilibrium. The depression is lowered to restore the equilibrium. The depression in freezing point in a dilute solution is proportional to molality of the solute.
The freezing point of a 5gCH3COOH(aq) per 100 g water is 1.576∘C. The van't Hoff factor (Kf of water =1.86Kmol−1 kg)A0.996B2C0.5D1.016When we add a non-volatile solute to a solvent lowers its vapour pressure. Therefore, the vapour pressure of a solution is lower than that of pure solvent, at the same temperature. A higher temperature is needed to raise the vapour pressure upto one atmosphere pressure, when boiling point is attained. However, b.pt. increases small. For example, 0.1 molal aqueous sucrose solution boils at 100.05∘C. Sea water, which is rich in Na+ and Cl− ions, freezes about 1∘C lower than freezes pure water. At the freezing point of a pure-solvent, the rates at which two molecule stick together to form the solute is present. Few solvent molecules are in constant with surface of solid. However, the rate at which the solvent molecules leave the surface of solid remains unchanged. That is why temperature is lowered to restore the equilibrium. The depression is lowered to restore the equilibrium. The depression in freezing point in a dilute solution is proportional to molality of the solute.
An aqueous solution of 0.1 molal concentration of sucrose should have freezing point (Kf=1.86Kmol−1kg)A0.186∘CB1.86∘CC−1.86∘CD−0.186∘CWhen we add a non-volatile solute to a solvent lowers its vapour pressure. Therefore, the vapour pressure of a solution is lower than that of pure solvent, at the same temperature. A higher temperature is needed to raise the vapour pressure upto one atmosphere pressure, when boiling point is attained. However, b.pt. increases small. For example, 0.1 molal aqueous sucrose solution boils at 100.05∘C. Sea water, which is rich in Na+ and Cl− ions, freezes about 1∘C lower than freezes pure water. At the freezing point of a pure-solvent, the rates at which two molecule stick together to form the solute is present. Few solvent molecules are in constant with surface of solid. However, the rate at which the solvent molecules leave the surface of solid remains unchanged. That is why temperature is lowered to restore the equilibrium. The depression is lowered to restore the equilibrium. The depression in freezing point in a dilute solution is proportional to molality of the solute.
When 250 mg of eugenol is added to 100 g of camphor (kf=39.7K molality−1), it lowered the freezing point by 0.62∘C. The molar mass of eugenol isA1.6×102g/molB1.6×104g/molC1.6×103g/molD200 g/mol
If an additional pressure Δp of a saturated vapour over a convex spherical surface of a liquid is considerably less than the vapour pressure over a plane surface, then Δp=(ρv/ρl)2α/r, where ρv and ρl) are the densities of the vapour and the liquid, α is the surface tension, and r is the radius of curvature of the surface. Using this formula, find the diameter of water droplets at which the saturated vapour pressure exceeds the vapour pressure over the plane surface by η=1.0% at a temperature t=27∘C. The vapour is assumed to be an ideal gas.
View SolutionAnswer question numbers (a) - (d) on the basis of your understanding of the following paragraph and the related studied concepts :
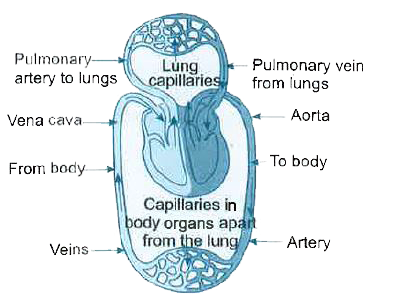
The separation of the right side and the left side of the heart is useful to keep oxygenated and de-oxygenated blook from mixing. Such separation alllows a highly efficient supply of oxygen to the body. This is useful in animals that have high energy needs, such as birds and mammals, which constantly use energy to maintain their body temperature. In animals that do not use energy for this purpose, the body temperature depends on the temperature in the environment . Such animals, like amphibians or many reptiles have three- chambrered hearts, and tolerate some mixing of the oxygenated and de-oxygenated blood streams. Fishes, on the other hand, have only two chambers to their hearts, and the blood is pumped to the gills, is oxygenated there, and passes directly to the rest of the body.
(a) What does the give diagram depict ?
(b) In which type of organisms would you find this type of transportation ?
(c) Explain why some animals like fishes have only two chambered heart ?
(d) From this study what can you deduct about evolution ?
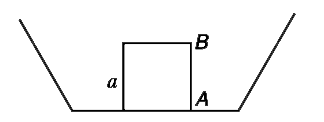
View Solution(i) A non uniform cube of side length a is kept inside a container as shown in the figure. The average density of the material of the cube is 2 ρ where ρ is the density of water. Water is gradually fille din the container. It is observed that the cube begins to topple, about its edge into the plane of the figure passing through pointA, when the height of the water in the container becomes a2. Find the distance of the centre of mass of the cube from the face AB of the cube. Assume that water seeps under the cube.
(ii) A rectangular concrete block (specific gravity =2.5) is used as a retatining wall in a reservoir of water. The height and width of the block are x and y respectively the height of water in the reservoir is z=34x. the concrete block cannot slide on the horizontal base but can rotate about an axis perpendicular to the plane of the figure and passing through point A
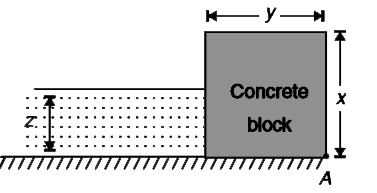
(a) Calculate the minimum value of the ratio yx for which the block will not begin to overturn about A.
(b) Redo the above problem for the case when there is a seepage and a thin film of water is present under the block. Assume that a seal at A prevents the water from flowing out underneath the block.
View SolutionA 500 g teapot and an insulated thermos are in a 20∘C room. The teapot is filled with 1000 g of the boiling water. 12 tea bags are then placed into the teapot. The brewed tea is allowed to cool to 80∘C, then 250 g of the tea is poured from the teapot into the thermos. The teapot is then kept on an insulated warmer that transfers 500 cal/min to the tea. Assume that the specific heat of brewed tea is the same as that of pure water, and that the tea bags have a very small mass compared to that of the water, and a negligible effect on the temperature. The specific heat of teapot is 0.17J/g K and that of water is 4.18J/g K. The entire procedure is done under atmospheric pressure. There are 4.18 J in one calorie.
An alternative method for keeping the tea hot would be, to place the teapot on a 10 pound block that has been heated in an oven to 300∘C. A block of which of the following substances would best be able to keep the tea hot?
View SolutionIn the case of immiscible liquids, the addition of one liquid to another does not after the properties of either liquid. Hence liquid exerts its own vapour pressure independently of the pressure of the other. Since boiling point of any system is the temperature at which its total vapour pressure becomes equal to the prevailing pressure, so by knowing the miscibility of two liquids, we can find out boiling temperature.
An immiscible mixture of water and quinoline is prepared and distillation is done. If p∘quinoline=7.9 torr and p∘water=732.04 torr at the boiling point of 98.9∘C. Find out the relative masses of water and quinoline in the distillate. If it is given that no of moles of any component in the vapour phase ∝ its vapour pressure. (Molar mass of water = 18 g/mol and molar mass of quinoline =129g/mol)
View Solution