In the figure, M is the mid point of CA.DM produced meet BA at B N also AN=AM, Prove that BDBN=DCCM.
Step by step video & image solution for In the figure, M is the mid point of CA. DM produced meet BA at B N also AN=AM, Prove that (BD)/(BN)= (DC)/(CM). by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Similar Questions
Knowledge Check
- Question 1 - Select One
In the given figure, M is the mid-point of both AC and BD. Then
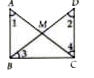 A∠1=∠2B∠1=∠4C∠2=∠4D∠1=∠3
A∠1=∠2B∠1=∠4C∠2=∠4D∠1=∠3 - Question 2 - Select One
ABCD is a parallelogram and M is the mid point of BC. AB and DM are produced to meet at N, then :
AA)AN=√3ABBB)AN=2ABCC)AN2=32AB2DD)AN2=2AB2 - Question 3 - Select One
ABCD is a parallelogram and M is the mid point of BC. AB and DM are produced to meet at N, then :
AAN=√3ABBAN=2ABCAN2=32AB2DAN2=2AB2
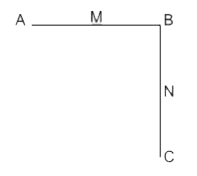
in figure , M is the mid-point of AB and N is the mid-point of BC (1) if AB=BC , prove that AM=NC
View Solutionin figure , M is the mid-point of AB and N is the mid-point of BC (1) if AB=BC , prove that AM=NC
View SolutionIn the give figure AB = BC, M is the mid point of AB and N is the mid point of BC, Show that AM = NC
 View Solution
View SolutionIn figure, P is the mid-point of BC,,Q is the mid-point of AP , such that BQ produced meets AC at R. Prove that 3RA=CA
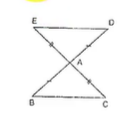
View SolutionIn Figure, the side BA and CA have been produced such that BA=AD and CA=AE. Prove that segment DE∣∣BC
 View Solution
View Solution



