P is a point on the parabola y2=4axandPQ is its focal chord. If PT is tangent at P and QN is normal at Q, the angle α, between PTandQN , distance between PT and QN is 'd' then
Step by step video & image solution for P is a point on the parabola y^2= 4ax and PQ is its focal chord. If PT is tangent at P and QN is normal at Q, the angle alpha, between PT and QN , distance between PT and QN is 'd' then by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
(0)2√1+1212 (C) 3 P is a point ‘t' on the parabola y2= 4ax and PQis a focal chord. PT is a tangent at P and QN is a normal at Q. The minimum distance between PT and QN is equal to 150 (B) a V1+t + (A) 0 1+ t2 a(t2 2
View SolutionIn Figure 1, O is the centre of a circle, PQ is a chord and PT is the tangent at P. If angle POQ = 70°, then angleTPQ is equal to
View Solution
Knowledge Check
In the figure , PQ is a chord of a circle and PT is a tangent at P such that ∠QPT=60∘, then ∠PRQ =
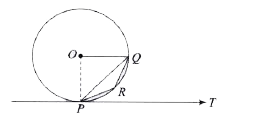 A100∘B110∘C120∘D150∘
A100∘B110∘C120∘D150∘Let PQ be a focal chord of the parabola y2=4ax such that tangents at P and Q meet at point on the line y=2x+a,a>0, If PQ subtends an angle θ at the vertex of y2=4ax, then tan θ=
A23√7B−23√7C23√5D−23√5At a point P on the parabola y2=4ax, tangent and normal are drawn. Tangent intersects the x-axis at Q and normal intersects the curve at R such that chord PQ subtends an angle of 90∘ at its vertex. Then
APQ=2a√6BPR=6a√3Carea of ΔPQR=18√2a2DPQ=3a√2
If PQ is the focal chord of the parabola y2=−xandP is (−4,2), then the ordinate of the point of intersection of the tangents at P and Q is
View SolutionIf PQ is the focal chord of the parabola y2=−xandP is (−4,2), then the ordinate of the point of intersection of the tangents at P and Q is
View SolutionIf the angle between the normal to the parabola y2=4ax at point P and the focal chord passing through P is 60∘, then find the slope of the tangent at point P.
View SolutionIf the angle between the normal to the parabola y2=4ax at point P and the focal chord passing through P is 60∘, then find the slope of the tangent at point P.
View SolutionLet PQ be a focal chord of the parabola y2=4ax The tangents to the parabola at P and Q meet at a point lying on the line y=2x+a,a>0. Length of chord PQ is
View Solution
