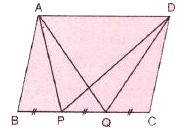
In a parallelogram ABCD, points P and Q are points of trisection of diagonal BD. Prove that CQ is parallel to AP.
ABCD is a parallelogram
P and Q are trisect points
DP=PQ=QB
DP+PQ=BQ+PQ
PQ=BP
In △APBand△CQD
AB=CD(opp. side of parallelogram)
BP=DQ(proved)
∠ABP=∠CDQ(alernative interior angles)
△APB≅△CQD
∠APB=∠CQD
But these angles are alternative interior angle
AP||CQ
Hence Proved
Similar Questions
In a parallelogram ABCD, X and Y are points on diagonal BD such that DX=BY. Prove that AXCY is a parallelogram.
View SolutionP and Q are the points of trisection of the diagonal BD of a parallelogram ABCD. Prove that CQ is parallel to AP.
View SolutionM and N are the points of trisection of the diagonal BD of a parallelogram ABCD. Prove that CN is parallel to AM.
View SolutionIn parallelogram ABCD, points P and Q lie on side BC and trisect it. Prove that :
ar.(ΔAPQ)=ar.(ΔDPQ)
=16×ar. (Parallelogram ABCD)
View SolutionP and Q are the points of trisection of the diagonal BD of a parallelogram ABCD. Prove that CQ is parallel to AP. Prove also that AC bisects PQ.
View SolutionP and Q are the points of trisection of the diagonal BD of a parallelogram ABCD. Prove that CQ is parallel to AP. Prove also that AC bisects PQ
View SolutionIn parallelogram ABCD two points P and Q are taken on diagonal BD such that DP = BQ (set figure). Show that:
(i)ΔAPD≅CQB(ii)AP=CQ(iii)ΔAQB≅ΔCPD(iv)AQ=CP(v)APCQis a parallelogram. ltbegt
View SolutionIn parallelogram ABCD two points P and Q are taken on diagonal BD such that DP = BQ (set figure). Show that:
(i)ΔAPD≅CQB(ii)AP=CQ(iii)ΔAQB≅ΔCPD(iv)AQ=CP(v)APCQis a parallelogram. ltbegt
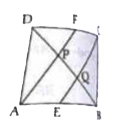
View SolutionIn a parallelogram ABCD, points E and F are respectively midpoint of sides AB and CD (see the adjacent figure). Prove that line segment AF and EC trisect diagonal BD.
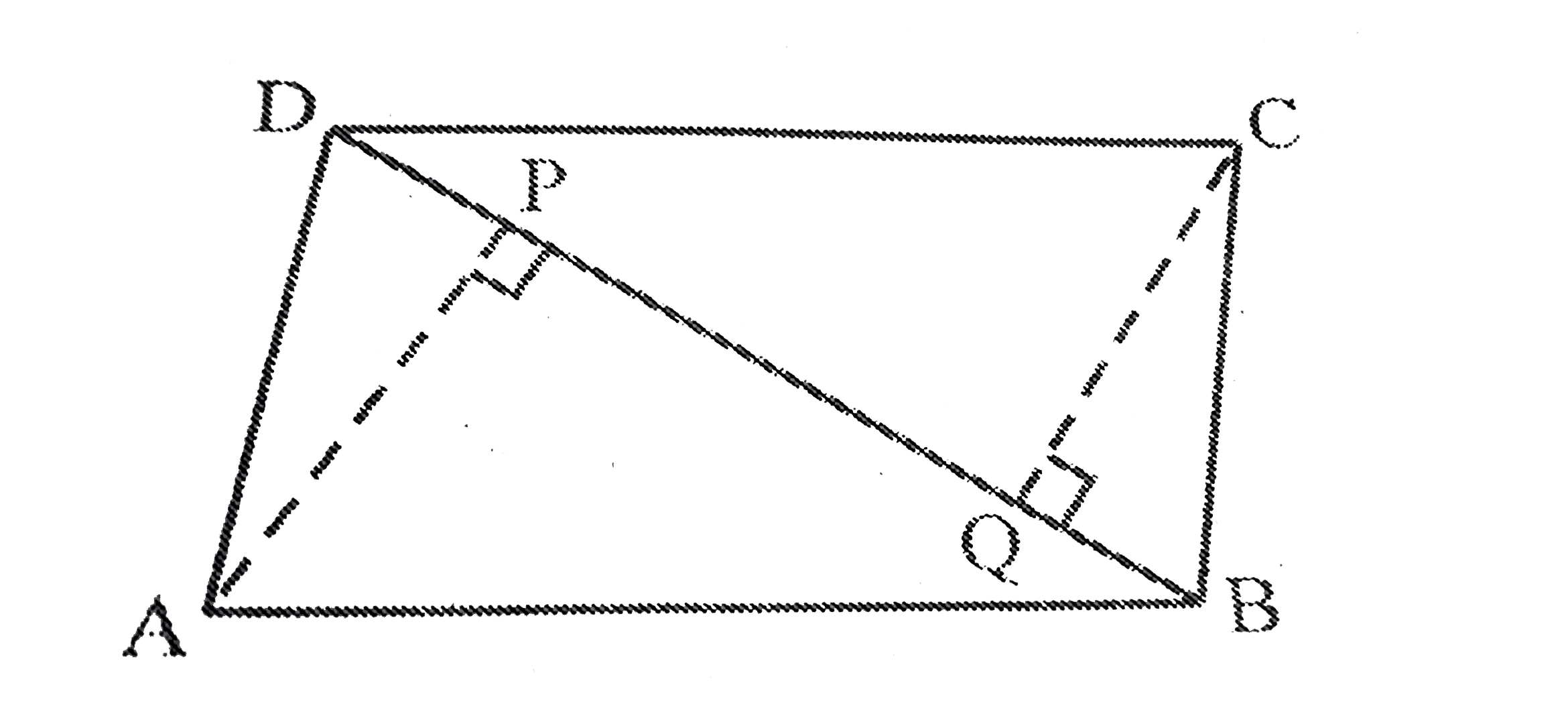
View SolutionABCD is a parallelogram and AP and CQ are perpendiculars from vertices A and C on diagonal BD . Show that
(i) ΔAPB≅ ΔCQD
(ii) AP = CQ
View Solution
