Question

फलन $f\left(x\right)=x^2+x-1$ के लिए अंतराल [0, 4] में लैग्रंजे के मध्यमान प्रमेय को सत्यापित कीजिए।

Explanation

दिया है: `f(x)=x^(2)+x-1` व अंतराल `[a, b]=[0, 4]`
`implies f'(x)=2x+1 implies a=0, b=4`
दिया गया फलन एक बहुपदीय फलन है इसलिए सर्वत्र सतत एवं अवकलनीय होगा।
`implies f(x)` लैग्रंजे के मध्यमान प्रमेय के सभी प्रतिबंधों को संतुष्ट करता है। अतः लैग्रंजे के मध्यमान प्रमेय से अंतराल [0, 4] में एक ऐसे c का अस्तित्व है जिसके लिए
`f'(c)=(f(b)-f(a))/(b-a)`

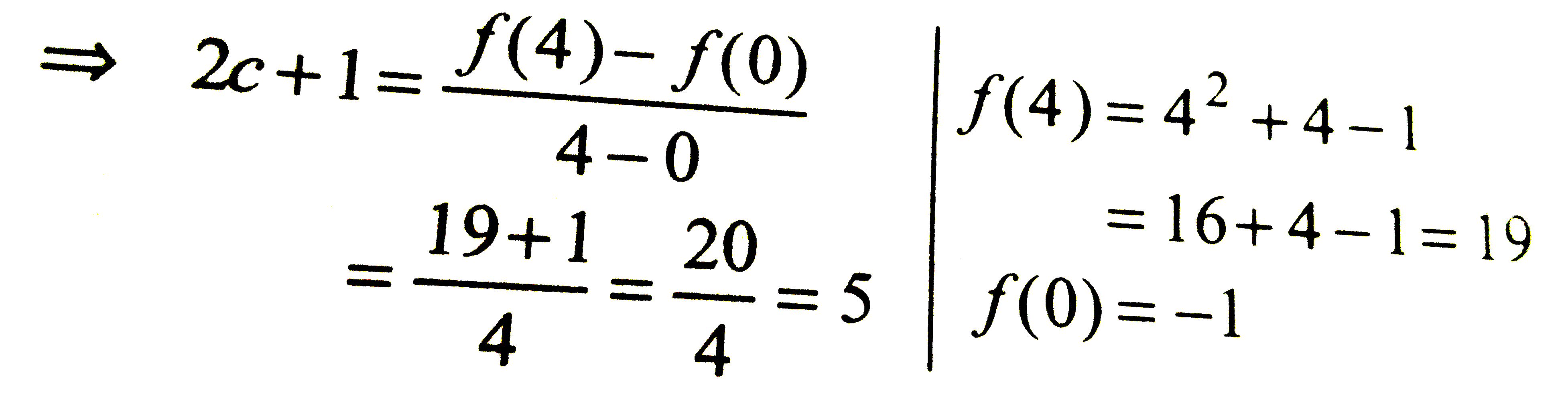
`implies 2c=5-1=4`
`c=4/2=2`
स्पष्टतः `c=2 in [0, 4]` अतः लैग्रंजे का मध्यमान प्रमेय सत्यापित होता है।