एक लंबवृत्तीय शंकु की तिर्यक ऊँचाई (slant height) दी हुई है सिद्ध कीजिये कि जब शंकु का आयतन महत्तम है तब शंकु का अर्द्धशीर्ष कोण tan−1(√2) होगा ।
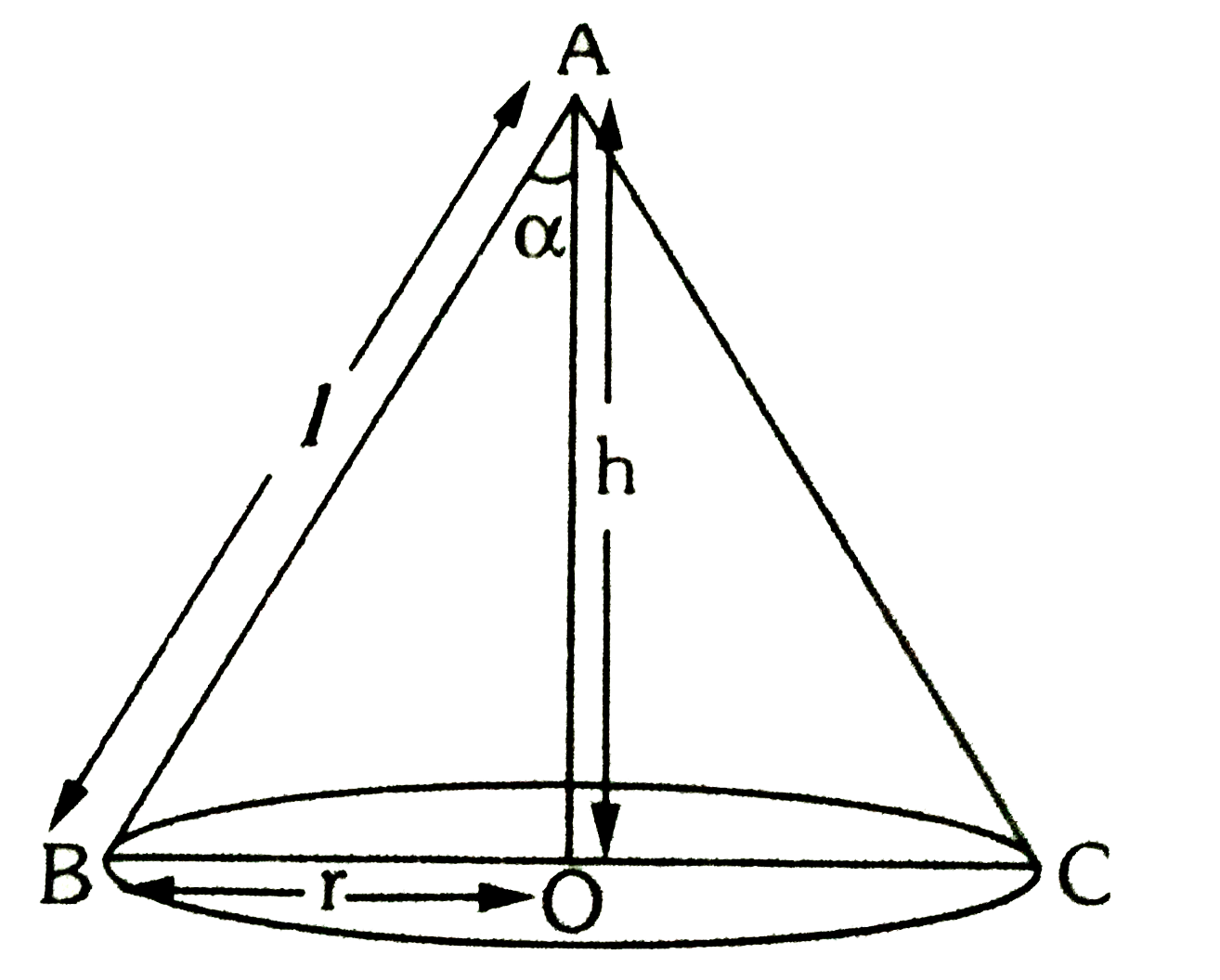
माना ABC अभीष्ट शंकु है जिनकी तिर्यक ऊँचाई AB = l ( दी हुई है ।)
माना शंकु का अर्द्धशीर्ष कोण ∠OAB=α,
माना आधार की त्रिज्या
OB = r
तथा ऊँचाई OA = h
अतः rl=sinα⇒r=lsinα
तथा OAAB=cosα
⇒OA=h=lcosα
यदि शंकु का आयतन V है तब
V=13πr2h (सूत्र )
=13πl2sin2αlcosα
V=13πl3sin2αcosα ...(1)
αके सापेक्ष अवकलन करने पर ,
dVdα=13πl3[2sinαcos2α−sin3α] ...(2)
तथा d2Vdα2
=13πl3[2cos3α−4sin4α−3sin2αcosα]
=13πl3[2cos3α−7sin2αcosα] ...(3)
आयतन 'V' के उच्चिष्ठ अथवा निम्निष्ठ मान के लिये dVdα=0
अतः समीकरण (2) से ,
13πl3sinα[2cos2α−sin2α]=0
⇒sinα=0⇒α=0( असंभव )
∴2cos2α−sin2α=0या tan2α=2
या tanα=√2⇒α=tan−1√2
α=tan−1√2 पर ,
d2Vdα2=13πl3[23√3−2×73√3]=−4πl33√3 ( ऋण राशि )
अतः शंकु का आयतन महत्तम होगा यदि शंकु का अर्द्धशीर्ष कोण tan−1√2 है ।
Topper's Solved these Questions
- उच्चिष्ठ एवं निम्निष्ठBOOK - BALAJI PUBLICATIONCHAPTER - उच्चिष्ठ एवं निम्निष्ठEXERCISE - विविध उदाहरण
25 Videos
- उच्चिष्ठ एवं निम्निष्ठBOOK - BALAJI PUBLICATIONCHAPTER - उच्चिष्ठ एवं निम्निष्ठEXERCISE - अभ्यास प्रश्न 11.1
18 Videos
- आव्यूह BOOK - BALAJI PUBLICATIONCHAPTER - आव्यूह EXERCISE - स्वमूल्यांकन परिक्षण
17 Videos
- खण्डश: समाकलन BOOK - BALAJI PUBLICATIONCHAPTER - खण्डश: समाकलन EXERCISE - स्वमूल्यांकन परीक्षण
28 Videos
Similar Questions
यदि फलन f(x)=x3−24x2+kx−8 बिंदु x = 2 पर उच्चिष्ठ है तो k का मान ज्ञात कीजिये ।
View Solutionx के किन मानों के लिये फलन उच्चिष्ठ अथवा निम्निष्ठ है ?
x3−3x2−9x
View Solutionप्रारंभिक स्तम्भ रूपांतरणों के प्रयोग द्वारा आव्यूह A=⎡⎢⎣012123311⎤⎥⎦ का व्युत्क्रम ज्ञात कीजिए।
View Solutionx sin x का समाकलन कीजिए-
View Solutionएक नली में 12 सेमी.3/से. कि दर से बालू उंडेली जा रही है। उंडेली गई बालू से एक शंकु का निर्माण इस प्रकार होता है कि शंकु कि ऊंचाई सदैव आधार कि त्रिज्या का 16 वा भाग होती ह। बालू के शंकु कि ऊंचाई में किस गति से वृद्धि हो रही है जबकि ऊंचाई 4 सेमी. है ?
View Solutionएक शंकु की त्रिज्या 7 सेमी और ऊँचाई 9 सेमी है। इसका आयतन समान त्रिज्या वाले एक दूसरे शंकु के वक्र पृष्ठ के बराबर होता है। इस शंकु को तिर्यक ऊँचाई ज्ञात कीजिए।
View Solutionशंकु का छिन्नक|छिन्नक का पृष्ठीय क्षेत्रफल एवं आयतन#!#उदाहरण
View SolutionRevision|शंकु का आयतन#!#महत्वपूर्ण प्रश्न
View Solutionबेलन का आयतन|उदाहरण#!#शंकु का आयतन
View Solutionशंकु का आयतन|उदाहरण
View Solutionशंकु एवं गोले का आयतन|उदाहरण
View Solutionशंकु का आयतन|गोले का आयतन#!#अर्धगोले का आयतन#!#महत्वपूर्ण प्रश्न
View Solutionपृष्ठीय क्षेत्रफल और आयतन|शंकु का आयतन#!#महत्वपूर्ण प्रश्न
View Solutionपृष्ठीय क्षेत्रफल और आयतन|शंकु का आयतन#!#शंकु के आयतन पर आधारित महत्वपूर्ण प्रश्न
View Solutionपृष्ठीय क्षेत्रफल और आयतन|शंकु का आयतन#!#महत्वपूर्ण प्रश्न
View Solutionपृष्ठीय क्षेत्रफल और आयतन#!#शंकु का पृषठीय क्षेत्रफल#!#शंकु का आयतन#!#परीक्षा के लिए प्रश्न
View Solution
