सिद्ध कीजिये कि एक गोले के अंतर्गत , जिसकी त्रिज्या है , उच्चतम आयतन के बने बेलन की ऊँचाई 2a√3 है ।
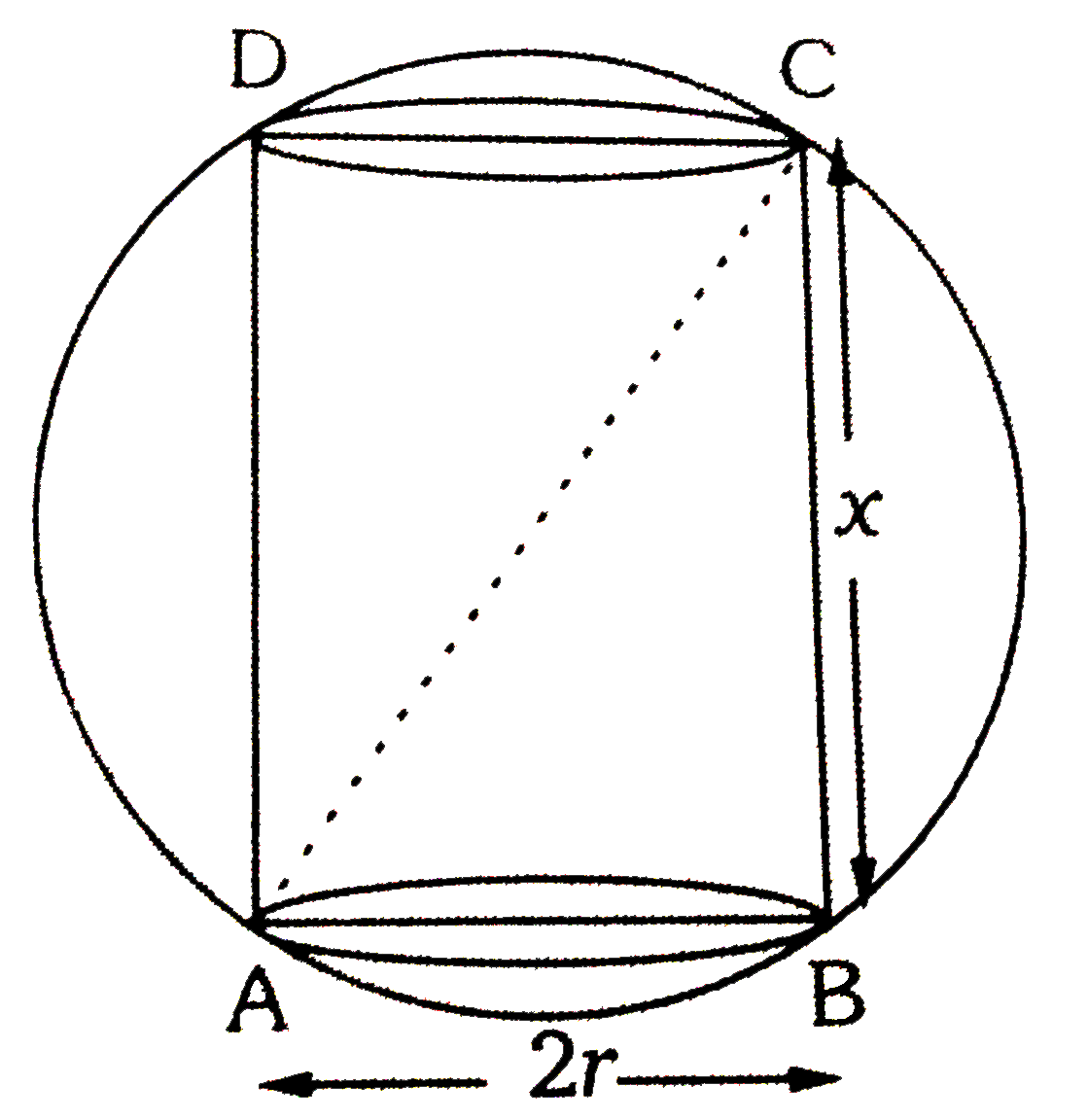
माना बेलन की आधार त्रिज्या r तथा ऊँचाई BC = x
गोले की त्रिज्या a है । अतः व्यास
AC = 2a,
समकोण ΔABC में ,
(AC)2=(AB)2+x2
⇒4a2−x2=4r2
⇒r2=4a2−x24 ...(1)
यदि बेलन का आयतन V है तब ,
V=π(4a2−x24)x⇒V=π4(4a2x−x3) .....(2)
दोनों पक्षों का xके सापेक्ष अवकलन करने पर ,
dVdx=π4(4a2−3x2) ...(3)
तथा d2Vdx2=π4(0−6x)=−32πx .....(4)
आयतन के उच्चिष्ठ अथवा निमनिष्ठ मान के लिये
dVdx=0,
अतः समीकरण (3) से , π4(4a2−3x2)=0
⇒x2=4a23⇒x=2a√3
x=2a√3पर , d2Vdx2=−32π×2a√3=−√3πa
अतः बेलन का आयतन महत्तम होगा यदि उसकी ऊँचाई 2a√3 है ।
Topper's Solved these Questions
- उच्चिष्ठ एवं निम्निष्ठBOOK - BALAJI PUBLICATIONCHAPTER - उच्चिष्ठ एवं निम्निष्ठEXERCISE - विविध उदाहरण
25 Videos
- उच्चिष्ठ एवं निम्निष्ठBOOK - BALAJI PUBLICATIONCHAPTER - उच्चिष्ठ एवं निम्निष्ठEXERCISE - अभ्यास प्रश्न 11.1
18 Videos
- आव्यूह BOOK - BALAJI PUBLICATIONCHAPTER - आव्यूह EXERCISE - स्वमूल्यांकन परिक्षण
17 Videos
- खण्डश: समाकलन BOOK - BALAJI PUBLICATIONCHAPTER - खण्डश: समाकलन EXERCISE - स्वमूल्यांकन परीक्षण
28 Videos
Similar Questions
यदि फलन f(x)=x3−24x2+kx−8 बिंदु x = 2 पर उच्चिष्ठ है तो k का मान ज्ञात कीजिये ।
View Solutionx के किन मानों के लिये फलन उच्चिष्ठ अथवा निम्निष्ठ है ?
x3−3x2−9x
View Solutionप्रारंभिक स्तम्भ रूपांतरणों के प्रयोग द्वारा आव्यूह A=⎡⎢⎣012123311⎤⎥⎦ का व्युत्क्रम ज्ञात कीजिए।
View Solutionx sin x का समाकलन कीजिए-
View Solutionसिद्ध कीजिये की बिंदु (1,−2),(3,6),(5,10) और (3,2) एक समांतर चतुर्भुज के शीर्ष है ।
View Solutionत्रिज्या r तथा ऊँचाई h वाले बेलन के लिए त्रिज्या के सापेक्ष पृष्ठीय क्षेत्रफल में परिवर्तन की दर ज्ञात करो।
View Solutionएक घनाकार सन्दूक के आयतन कि गणन में प्रतिशत त्रुटि ज्ञात कीजिये यदि घन कि कोर कि लम्बाई में त्रुटि 5 प्रतिशत रहती है।
View Solutionएक गोले कि त्रिज्या 7 सेमी. मापी जाती है जिसमे 0.02 सेमी. कि त्रुटि है। इस त्रुटि के कारण इसके आयतन कि गणना में सनिकटन त्रुटि ज्ञात कीजिए।
View Solutionएक घनाकार संदूक के आयतन कि गणना में प्रतिशत त्रुटि ज्ञात कीजिये, जबकि घन कि कोर कि लम्बाई में त्रुटि 5 प्रतिशत होती है।
View Solutionसिद्ध कीजिये x>0 की के लिए f(x)=1x हस्यमान फलां है।
View Solutionएक वृत्त के अंतर्गत बने समबहुभुज की प्रत्येक भुजा केंद्र पर 45∘ का कोण बनाती है| बहुभुज का नाम दीजिए |
View Solutionसिद्ध कीजिये कि3−2√5 एक अपरिमेय संख्या है।
View Solutionएक शंकु की त्रिज्या 7 सेमी और ऊँचाई 9 सेमी है। इसका आयतन समान त्रिज्या वाले एक दूसरे शंकु के वक्र पृष्ठ के बराबर होता है। इस शंकु को तिर्यक ऊँचाई ज्ञात कीजिए।
View Solutionएक धातु के बेलन को, जिसका व्यास 8 से.मी. और ऊँचाई 90 से. मी. है, गलाकर 12 से. मी. व्यास वाले कितने गोले बनाए जा सकते हैं ?
View SolutionA cylinder of radius 4.5 cm and height 12 cm just fits in another cylinder completely with their axis perpendicular. What is the radius (in cm) of second cylinder? एक बेलन जिसकी त्रिज्या 4.5 से.मी. तथा ऊँचाई 12 से.मी. है, को एक अन्य बेलन में उनके अक्षों के लम्बवत् पूरी तरह से सम्माहित किया गया है। दूसरे बेलन की त्रिज्या (से.मी. में) क्या है?
View SolutionA regular pyramid has a square base. The height of the pyramid is 22 cm and side of its base is 14 cm. Volume of pyramid is equal to the volume of a sphere. What is the radius (in cm) of the sphere?
एक सम पिरामिड का आधार एक वर्ग है। पिरामिड को ऊँचाई 22 से.मी. है तथा उसके आधार की भुजा 14 से.मी. है। पिरामिड का आयतन एक गोले के आयतन के बराबर हैं गोले की त्रिज्या (से.मी. में) क्या है?
View Solution
