सिद्ध कीजिये कि महत्तम क्षेत्रफल वाला आयत जो वृत्त में अंतर्निहित किया जा सके के वर्ग होता है ।
माना ABCD अभीष्ट आयतन है जिसके परिवृत्त की त्रिज्या a है तथा O केंद्र है माना OX तथा OY निर्देशाक्ष है । माना A(x, y) आयतन का एक शीर्ष है तब तथा
तथा
यदि आयत ABCD का क्षेत्रफल A है तब
...(1)
दोनों पक्षों का के सापेक्ष अवकलन करने पर
....(2)
तथा ....(3)
A के उच्चिष्ठ अथवा निमनिष्ठ मान के लिये
( ऋण राशि )
अतः पर आयत ABCD का क्षेत्रफल महत्तम होगा ।
पुनः
तथा
, अतः आयत ABCD एक वर्ग है ।
अतः वृत्त में बने महत्तम क्षेत्रफल का आयत एक वर्ग होता है ।

Topper's Solved these Questions
- BOOK - BALAJI PUBLICATIONCHAPTER - उच्चिष्ठ एवं निम्निष्ठEXERCISE - विविध उदाहरण25videos
उच्चिष्ठ एवं निम्निष्ठ
- BOOK - BALAJI PUBLICATIONCHAPTER - उच्चिष्ठ एवं निम्निष्ठEXERCISE - अभ्यास प्रश्न 11.118videos
उच्चिष्ठ एवं निम्निष्ठ
- BOOK - BALAJI PUBLICATIONCHAPTER - आव्यूह EXERCISE - स्वमूल्यांकन परिक्षण17videos
आव्यूह
- BOOK - BALAJI PUBLICATIONCHAPTER - खण्डश: समाकलन EXERCISE - स्वमूल्यांकन परीक्षण28videos
खण्डश: समाकलन
Similar Questions
यदि फलन f(x)=x3−24x2+kx−8 बिंदु x = 2 पर उच्चिष्ठ है तो k का मान ज्ञात कीजिये ।
03:28View Solutionx के किन मानों के लिये फलन उच्चिष्ठ अथवा निम्निष्ठ है ?
x3−3x2−9x02:43View Solutionप्रारंभिक स्तम्भ रूपांतरणों के प्रयोग द्वारा आव्यूह A=⎡⎢⎣012123311⎤⎥⎦ का व्युत्क्रम ज्ञात कीजिए।
02:12View Solutionx sin x का समाकलन कीजिए-
05:14View Solutionमहत्तम समापवर्तक क्या होता है ?
03:00View Solutionसिद्ध कीजिये कि (0,2π) में फलन f(x)=x−sinx वर्धमान है।
45:35View Solutionसिद्ध कीजिये कि प्रदत फलन f(x)=cosx
(0, pi) में निरंतर हस्यमान है।46:53View Solutionएक फूलों की क्यारी, जो एक वृत्त के त्रिज्याखण्ड के रूप में है, की घेराबंदी करने के लिए 20 मीटर तार उपलब्द है। तो फूलों की क्यारी का अधिकतम क्षेत्रफल (वेग मी) में है
02:50View Solutionसिद्ध कीजिये की दो विषय संख्याओं का योग सम होता है।
04:03View Solutionसमतल आकृतियों का क्षेत्रफल |आयत , वर्ग , त्रिभुज तथा वृत्त का क्षेत्रफल #!#कुछ अभ्यास प्रश्न
01:41View Solutionसमतल आकृतियाँ |आयत ,वर्ग वृत्त तथा त्रिभुज #!#परिमाप और क्षेत्रफल
03:36View SolutionIn the given figure, PQR is a quadrant whose radius is 7cm.A circle is incribed in the quadrant as shown in the figure.What is the area (in cm2) of the circle?
दी गई आकृति में, PQR एक वृत्त-खण्ड है जिसकी त्रिज्या 7 से.मी. है। जेसा कि आकृति में दर्शाया गया है कि वृत्त-खण्ड में एक वृत्त को अंकित किया गया हें वृत्त का क्षेत्रफल (से.मी.2 में) क्या है?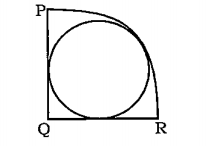 01:36View Solution
01:36View SolutionThe perimeter of a rectangle is 50 cm. Its area and length are in the ratio of 5:1. Find the length of the rectangle?
एक आयत की परिधि 50 सेमी है। इसका क्षेत्रफल और लंबाई 5: 1 के अनुपात में है। आयत की लंबाई ज्ञात कीजिये?01:55View SolutionIf the perimeter and length of a rectangle are in the ratio 6:1 and the area of the rectangle is 288cm2. Find the length of the rectangle.
यदि आयत की परिधि और लंबाई 6: 1 के अनुपात में है और आयत का क्षेत्रफल 288 वर्ग सेमी है। आयत की लंबाई ज्ञात कीजिए।02:33View SolutionIn the given figure, the ratio of the area of the largest square to that of the smallest square is: दी गयी आकृति में, सबसे बड़े वर्ग के क्षेत्रफल और सबसे छोटा वर्ग के क्षेत्रफल का अनुपात है
01:32View SolutionThe perimeter and length of a rectangle are in the ratio of 8:1, and the area of the rectangle is 1323cm2. Find the length of the rectangle.
एक आयत का परिमाप और उसकी लंबाई 8:1 के अनुपात में है। आयत का क्षेत्रफल 1323 वर्ग सेमी है। आयत की लंबाई ज्ञात कीजिए।32:35View Solution
