सिद्ध कीजिये कि किसी दिये हुए गोले के अंतर्गत महत्तम आयतन के शंकु की ऊँचाई का गोले के व्यास से अनुपात $2 : 3$ होता है ।

Video Solution

Text Solution

Verified by Experts

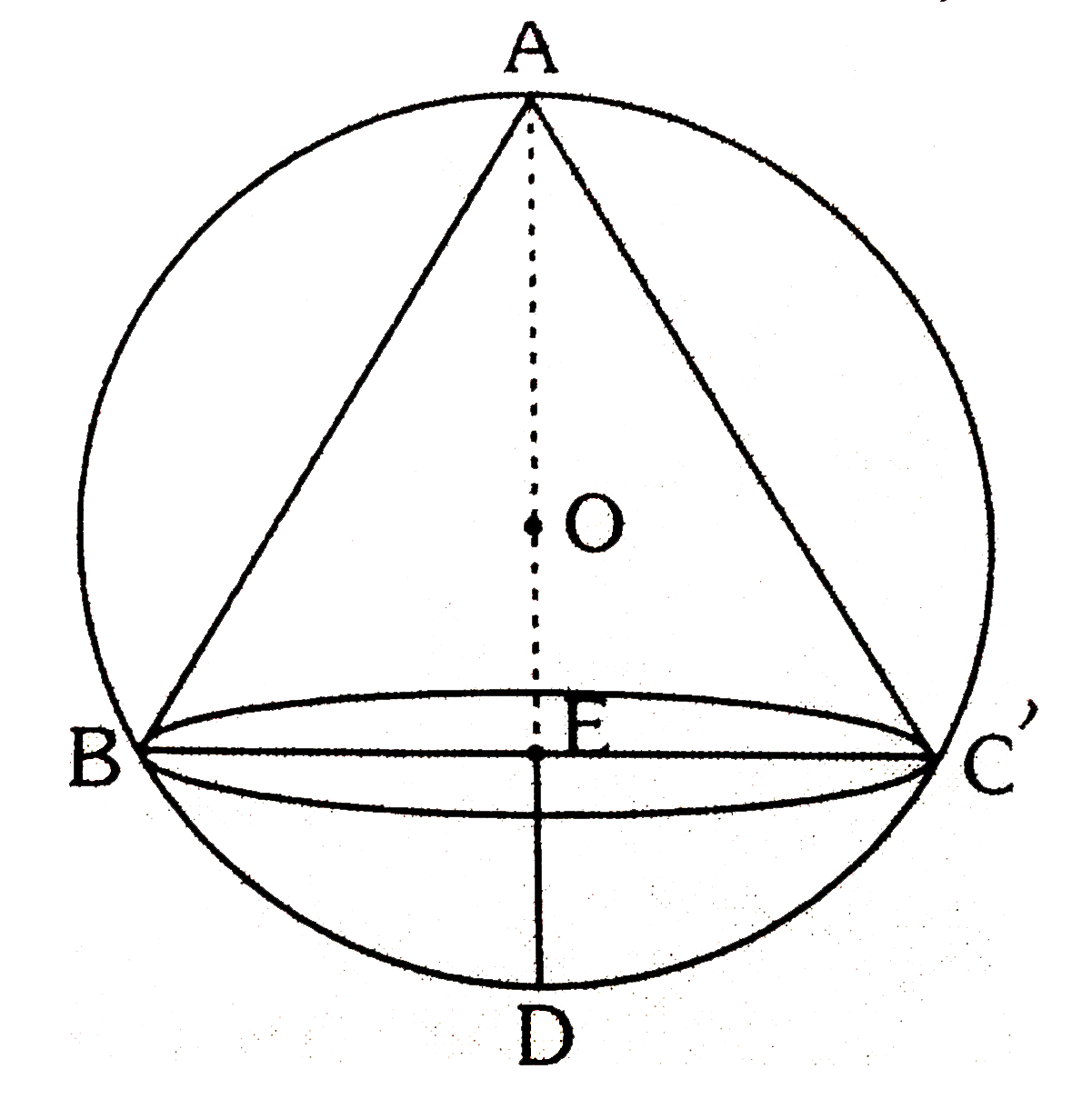
माना ABC अभीष्ट शंकु है तथा 'O' अभीष्ट गोले का केंद्र है । माना गोले की त्रिज्या r है । शंकु का आयतन महत्तम होगा यदि शंकु का शीर्ष A गोले के ऊर्ध्वाधर व्यास के उच्चतम बिंदु 'A' पर स्थित है । माना शंकु की ऊँचाई AE = h तथा आधार त्रिज्या BE = x, अतः ज्यामिति से
$B E \times C E = A E \times E D$
$\Rightarrow x^{2} = h (2 r - h)$
यदि शंकु का आयतन V है तब
$V = \frac{1}{3} π x^{2} h$
$\Rightarrow V = \frac{1}{3} π h (2 r - h) h$
$V = \frac{1}{3} π [2 r h^{2} - h^{3}]$ ....(1)
दोनों पक्षों का के सापेक्ष अवकलन करने पर ,
$\frac{d V}{d h} = \frac{1}{3} π [4 r h - 3 h^{2}]$ ...(2)
तथा $\frac{d^{2} V}{d h^{2}} = \frac{1}{3} π [4 r - 6 h]$ ....(3)
आयतन 'V' के उच्चिष्ठ अथवा निम्निष्ठ मान के लिये
$\frac{d V}{d h} = 0$
अतः समीकरण (2) से ,
$\frac{1}{3} π h (4 r - 3 h) = 0$
$∴ 4 r - 3 h = 0 (. ∵ h \neq 0)$
या $r = \frac{3}{4} h या 2 \times व्यास = 3 \times ऊँचाई$
$∴ \frac{शंकु की ऊँचाई}{गोले का व्यास} = \frac{2}{3}$
$\Rightarrow$ शंकु की ऊँचाई : गोले का व्यास = 2 : 3
समीकरण (3) से ,
$\frac{d^{2} V}{d h^{2}} = \frac{1}{3} π [4 \times \frac{3}{4} h - 6 h] = - π h$ = ( ऋण राशि )
अतः आयतन महत्तम होगा । अतः शंकु के महत्तम आयतन के लिये
शंकु की ऊँचाई : गोले का व्यास = 2 : 3

|

Updated on:21/07/2023

Class 12 MATHS APPLICATION OF DERIVATIVES

Topper's Solved these Questions

Similar Questions

BALAJI PUBLICATION-उच्चिष्ठ एवं निम्निष्ठ-स्वमूल्यांकन परीक्षण

Home
Ask Doubt
Profile