सिद्ध कीजिये कि शंकु के अंतर्गत बने लंबवृत्तीय बेलन का वक्रपृष्ठ महत्तम होगा यदि बेलन कि त्रिज्या शंकु की त्रिज्या की आधी है ।
माना शंकु की ऊँचाई h है । माना PARS अभीष्ट बेलन है ।
माना शंकु का अर्द्धशीर्ष कोण 'α' है तथा बेलन की आधार त्रिज्या x है ।
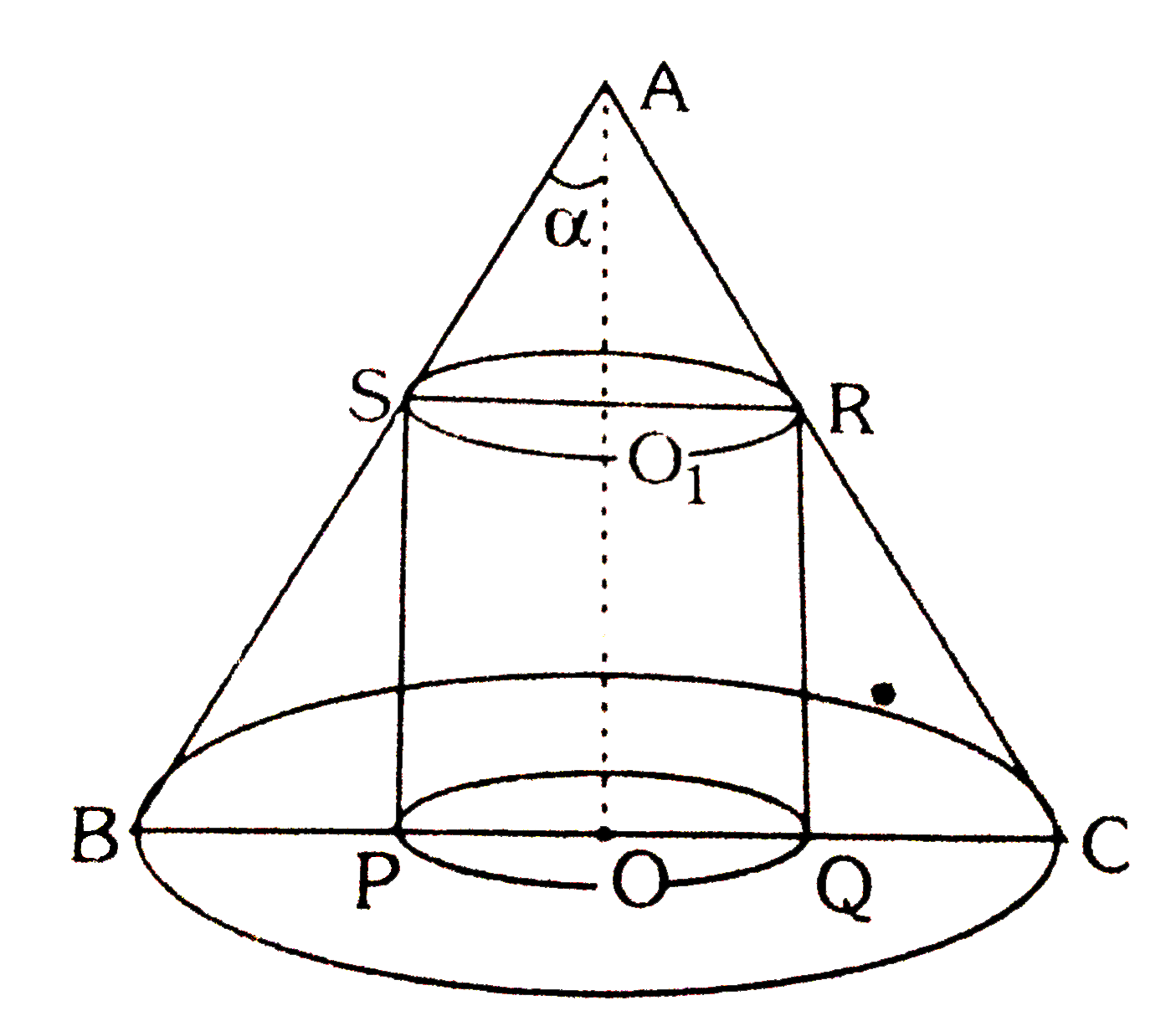
ΔASO1में ,AO1x=cotα⇒AO1=xcotα
बेलन की ऊँचाई
OO1=AO−AO1=(h−xcotα)
माना बेलन का वक्रपृष्ठ (curved surface) C है
तब C = आधार का परिमाप × ऊँचाई
⇒C=2πx(h−xcotα)
⇒C=2π(hx−x2cotα) ....(1)
दोनों पक्षों का x के सापेक्ष अवकलन करने पर ,
dCdx=2π(h−2xcotα) ...(2)
तथा d2Cdx2=2π(0−2cotα)
⇒d2Cdx2=−4πcotα ....(3)
'C' के उच्चिष्ठ अथवा निम्निष्ठ मान के लिये ,
dCdx=0
अतः समीकरण (2) से ,
2π(h−2xcotα)=0
⇒cotα=h2x
चित्र से , cotα=hOB
⇒h2x=hOB⇒OB=2x
अर्थात शंकु की आधार त्रिज्या OB बेलन की आधार त्रिज्या से दुगनी है ।
पुनः जब cotα=h2x
तब d2Cdx2=−4π(h2x)
=−2πhx ( ऋण राशि )
अतः जब शंकु की त्रिज्या बेलन की दुगनी है तो शंकु के अंतर्गत बने लंबवृत्तीय बेलन का वक्रपृष्ठ महत्तम होगा ।
Topper's Solved these Questions
- उच्चिष्ठ एवं निम्निष्ठBOOK - BALAJI PUBLICATIONCHAPTER - उच्चिष्ठ एवं निम्निष्ठEXERCISE - विविध उदाहरण
25 Videos
- उच्चिष्ठ एवं निम्निष्ठBOOK - BALAJI PUBLICATIONCHAPTER - उच्चिष्ठ एवं निम्निष्ठEXERCISE - अभ्यास प्रश्न 11.1
18 Videos
- आव्यूह BOOK - BALAJI PUBLICATIONCHAPTER - आव्यूह EXERCISE - स्वमूल्यांकन परिक्षण
17 Videos
- खण्डश: समाकलन BOOK - BALAJI PUBLICATIONCHAPTER - खण्डश: समाकलन EXERCISE - स्वमूल्यांकन परीक्षण
28 Videos
Similar Questions
यदि फलन f(x)=x3−24x2+kx−8 बिंदु x = 2 पर उच्चिष्ठ है तो k का मान ज्ञात कीजिये ।
View Solutionx के किन मानों के लिये फलन उच्चिष्ठ अथवा निम्निष्ठ है ?
x3−3x2−9x
View Solutionप्रारंभिक स्तम्भ रूपांतरणों के प्रयोग द्वारा आव्यूह A=⎡⎢⎣012123311⎤⎥⎦ का व्युत्क्रम ज्ञात कीजिए।
View Solutionx sin x का समाकलन कीजिए-
View Solutionत्रिज्या r तथा ऊँचाई h वाले बेलन के लिए त्रिज्या के सापेक्ष पृष्ठीय क्षेत्रफल में परिवर्तन की दर ज्ञात करो।
View Solutionएक नली में 12 सेमी.3/से. कि दर से बालू उंडेली जा रही है। उंडेली गई बालू से एक शंकु का निर्माण इस प्रकार होता है कि शंकु कि ऊंचाई सदैव आधार कि त्रिज्या का 16 वा भाग होती ह। बालू के शंकु कि ऊंचाई में किस गति से वृद्धि हो रही है जबकि ऊंचाई 4 सेमी. है ?
View Solutionएक शंकु की त्रिज्या 7 सेमी और ऊँचाई 9 सेमी है। इसका आयतन समान त्रिज्या वाले एक दूसरे शंकु के वक्र पृष्ठ के बराबर होता है। इस शंकु को तिर्यक ऊँचाई ज्ञात कीजिए।
View Solutionयदि शंकु की त्रिज्या 5 से. मी. हो, तो उसका व्यास होगा
View Solutionयदि बेलन का व्यास 20 से. मी. है, तो उसकी त्रिज्या होगी
View Solutionबेलन का आयतन|उदाहरण#!#शंकु का आयतन
View Solutionबेलन तथा शंकु
View SolutionA hollow cylinder of thickness 0.7 cm and height 15cm is made of iron. If inner radius of cylinder is 3.5 cm, then what is the total surface area (in cm^2 ) of the hollow cylinder? एक लोहे से बने बेलन की चौड़ाई 0.7 सेमी. तथा ऊँचाई 15 सेमी. है। यदि बेलन की आंतरिक त्रिज्या 3.5 सेमी. है, वो खाली बेलन का कुल पृष्ठीय क्षेत्रफल ( सेमी^2 में) क्या है?
View SolutionFrom a circular sheet of paper of radius 10cm, a sector of area 40% is removed. If the remaining part is used to make a conical surface, then the ratio of the radius and the height of the cone is- किसी कागज की गोलाकार सीट जिसकी त्रिज्या 10 सेमी से वृत्त खंड का 40% हटा दिया जाता है, यदि शेष हिस्से का प्रयोग करके एक शंकु बनाया जाता है, तो शंकु की त्रिज्या तथा ऊँचाई का अनुपात है।
View SolutionThe heights of a cone, cylinder and hemisphere are equal. If their radii are in the ratio 2:3:1, then the ratio of the their volumes is एक शंकु, बेलन तथा गोलार्द्ध की ऊँचाई बराबर हैं। यदि उनकी त्रिज्या 2: 3: 1 के अनुपात में है, तो उनके आयतनों का अनुपात है:
View SolutionThe volume of a right circular cone is equal to that of a sphere, whose radius is half the radius of the base of the cone. What is the ratio of the radius of the base to the height of the cone ?
एक लम्ब वृत्तीय शंकु का आयतन उस गोले के आयतन के बराबर है, जिसकी त्रिज्या शंकु के आधार की त्रिज्या से आधी है | शंकु के आधार की त्रिज्या और शंकु की ऊंचाई में क्या अनुपात है ?
View SolutionIf the radius of the base of a cone is doubled, and the volume of the new cone is three times the volume of the original cone, then what will be the ratio of the height of the original cone to that of the new cone ?
यदि किसी शंकु के आधार की त्रिज्या दोगुनी कर दी गयी है , और नए शंकु का आयतन आरंभिक शंकु के आयतन का तिगुना है, तो आरंभिक शंकु और नए शंकु की ऊँचाइयों के बीच क्या अनुपात होगा ?
View Solution
