सिद्ध कीजिये कि लम्ब वृत्ताकार शंकु के अंतर्गत बने महत्तम बेलन का आयतन 427πh3tan2α है जबकि शंकु की ऊँचाई h तथा अर्द्धशीर्ष कोण α है ।
माना 'ABC' अभीष्ट लंबवृत्तीय शंकु है जिसकी ऊँचाई AO = h तथा अर्द्धशीर्ष कोण α है । माना बेलन PQRS की त्रिज्या x है ।
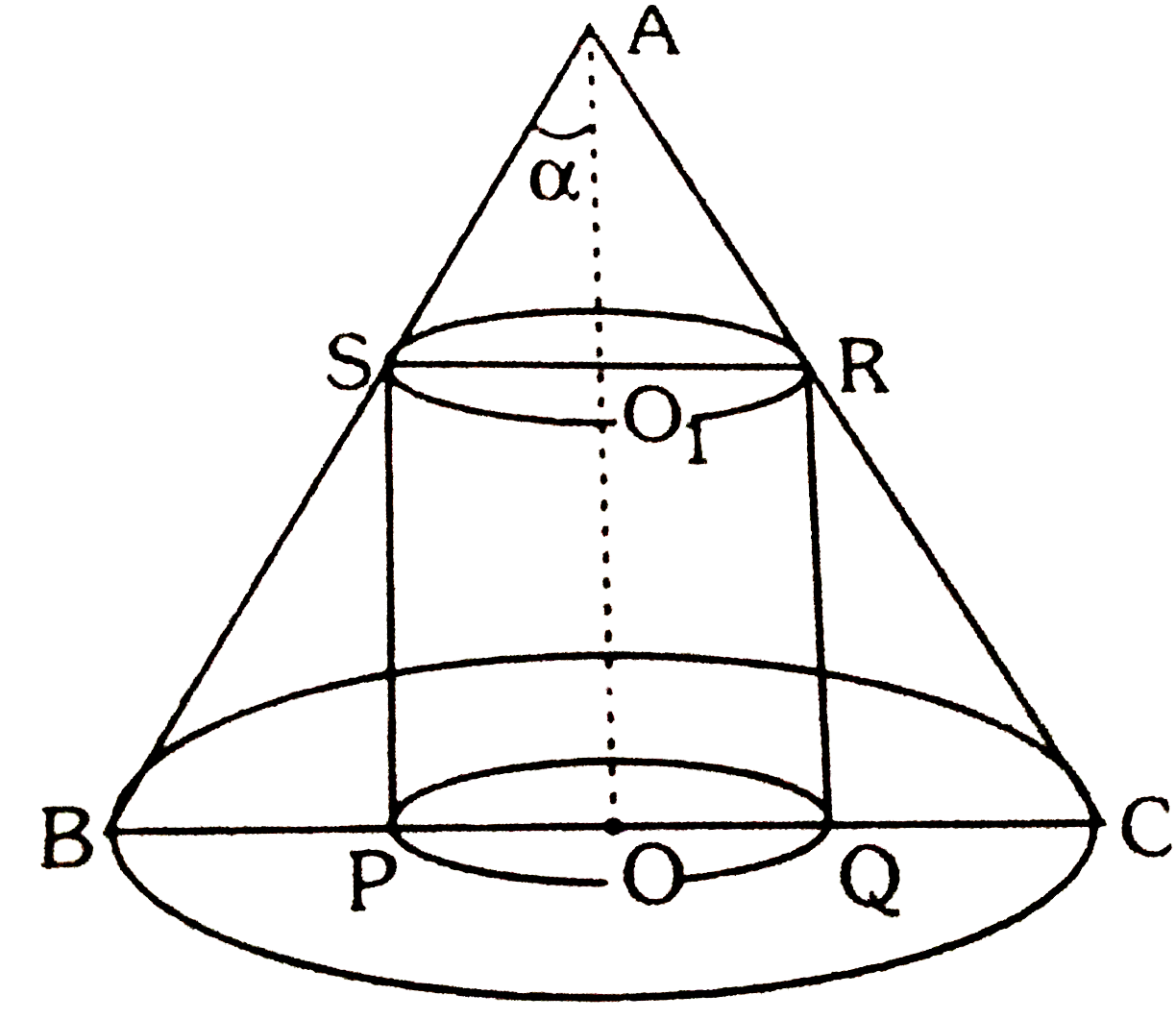
ΔASO1में , AO1x=cotα⇒AO1=xcotα
बेलन की ऊँचाई OO1=h−AO1=(h−xcotα)
यदि बेलन का आयतन V है तब
V=πx2(h−xcotα)
⇒V=π(hx2−x3cotα) ...(1)
दोनों पक्षों का x के सापेक्ष अवकलन करने पर ,
dVdx=π(2hx−3x2cotα) ....(2)
तथा d2Vdx2=π(2h−6xcotα) ...(3)
आयतन 'V' के उच्चिष्ठ एवं निम्निष्ठ मान के लिये dVdx=0
अतः समीकरण (2) से ,
πx(2h−3xcotα)=0
x=0 या x=2h3tanα
समीकरण (3) में ,x=2h3tanα रखने पर ,
d2Vdx2=π(2h−6×2h3tanαcotα)
=−2πh ( ऋण राशि ) उच्चिष्ठ
अतः x=2h3tanα पर बेलन का आयतन उच्चिष्ठ है । बेलन का उच्चिष्ठ आयतन समीकरण (1) से
V=π[h×4h29tan2α−8h327tan3α⋅cotα]
=πh3tan2α(49−827)=427πh3tan2α
Topper's Solved these Questions
- उच्चिष्ठ एवं निम्निष्ठBOOK - BALAJI PUBLICATIONCHAPTER - उच्चिष्ठ एवं निम्निष्ठEXERCISE - विविध उदाहरण
25 Videos
- उच्चिष्ठ एवं निम्निष्ठBOOK - BALAJI PUBLICATIONCHAPTER - उच्चिष्ठ एवं निम्निष्ठEXERCISE - अभ्यास प्रश्न 11.1
18 Videos
- आव्यूह BOOK - BALAJI PUBLICATIONCHAPTER - आव्यूह EXERCISE - स्वमूल्यांकन परिक्षण
17 Videos
- खण्डश: समाकलन BOOK - BALAJI PUBLICATIONCHAPTER - खण्डश: समाकलन EXERCISE - स्वमूल्यांकन परीक्षण
28 Videos
Similar Questions
यदि फलन f(x)=x3−24x2+kx−8 बिंदु x = 2 पर उच्चिष्ठ है तो k का मान ज्ञात कीजिये ।
View Solutionx के किन मानों के लिये फलन उच्चिष्ठ अथवा निम्निष्ठ है ?
x3−3x2−9x
View Solutionप्रारंभिक स्तम्भ रूपांतरणों के प्रयोग द्वारा आव्यूह A=⎡⎢⎣012123311⎤⎥⎦ का व्युत्क्रम ज्ञात कीजिए।
View Solutionx sin x का समाकलन कीजिए-
View Solutionएक नली में 12 सेमी.3/से. कि दर से बालू उंडेली जा रही है। उंडेली गई बालू से एक शंकु का निर्माण इस प्रकार होता है कि शंकु कि ऊंचाई सदैव आधार कि त्रिज्या का 16 वा भाग होती ह। बालू के शंकु कि ऊंचाई में किस गति से वृद्धि हो रही है जबकि ऊंचाई 4 सेमी. है ?
View Solutionएक वृत्त के अंतर्गत बने समबहुभुज की प्रत्येक भुजा केंद्र पर 45∘ का कोण बनाती है| बहुभुज का नाम दीजिए |
View Solutionएक शंकु की त्रिज्या 7 सेमी और ऊँचाई 9 सेमी है। इसका आयतन समान त्रिज्या वाले एक दूसरे शंकु के वक्र पृष्ठ के बराबर होता है। इस शंकु को तिर्यक ऊँचाई ज्ञात कीजिए।
View Solutionबेलन का आयतन|उदाहरण#!#शंकु का आयतन
View Solutionशंकु का आयतन|उदाहरण
View Solutionपृष्ठीय क्षेत्रफल और आयतन|शंकु का आयतन#!#शंकु के आयतन पर आधारित महत्वपूर्ण प्रश्न
View Solutionबेलन तथा शंकु
View Solutionपृष्ठीय क्षेत्रफल और आयतन#!#शंकु का पृषठीय क्षेत्रफल#!#शंकु का आयतन#!#परीक्षा के लिए प्रश्न
View Solutionपृष्ठीय क्षेत्रफल और आयतन#!#शंकु का पृष्ठीय क्षेत्रफल#!#शंकु का आयतन#!#परीक्षा के लिए महत्वपूर्ण प्रश्न
View SolutionThe lateral surface area of frustum of a right circular cone, if the area of its base is 16 pi cm^2 and the diameter of circular upper surface is 4cm and stant height 6 cm, will be किसी लम्ब वृत्ताकार शंकु के छिननक के पार्श्व सतह का क्षेत्रफल क्या होगा, जिसके आधार का क्षेत्रफल 16 pi से.मी.^2 है, वृत्ताकार उपरी सतह का व्यास 4 से.मी. है और तिरछी ऊँचाई 6 से.मी. है?
View SolutionThe numerical values of the volume and the area of the lateral surface of a right circular cone are equal if the height of the cone be h and radius be r, the value of 1/h^2+1/r^2 is- एक लंब चृत्तीय शंकु के आयतन और क्षेत्रफल पारश्वीय पृष्ठ के संख्यात्मक मान समान है। यदि शंकु की ऊंचाई h और त्रिज्या r है, तो 1/h^2+1/r^2 का मान है-
View SolutionThe volume of a right circular cone is equal to the volume of a right circular cylinder. The height and the radius of the cylinder are 9 cm and 20 cm respectively. If the height of the cone is 108 cm, then its radius (in cm) is- लंब वृत्ताकार शंकु का आयतन लंब वृत्ताकार सिलेंडर के आयतन बराबर है। सिलेंडर की ऊँचाई और त्रिज्या क्रमशः 9 सेमी और 20 सेमी हैं। यदि शंकु की ऊचाई 108 सेमी है, तो उसकी त्रिज्या कितनी (सेमी में) होगी?
View Solution
