सिद्ध कीजिए कि परवलयों y2=4ax तथा x2=4ay के बीच के क्षेत्रफल 163a2 होगा |
वक्रो के समीकरण y2=4ax ... (1)
तथा x2=4ay ... (2)
समीकरण (2 ) का वर्ग करने पर
x4=16a2y2=16a2⋅4ax [समीकरण (1 ) से ]
⇒x4=64a3x
⇒x(x3−64a3)=0
∴x=0 या x = 4a , जब x = 0 तब y = 0 [समी० (1) से ]
समीकरण (2 ) में x = 4a रखने पर, y=4a
अतः वक्रों के प्रतिच्छेद बिंदु O( 0, 0) तथा A (4a, 4a) है| A से x - अक्ष पर AM लम्ब डालिये |
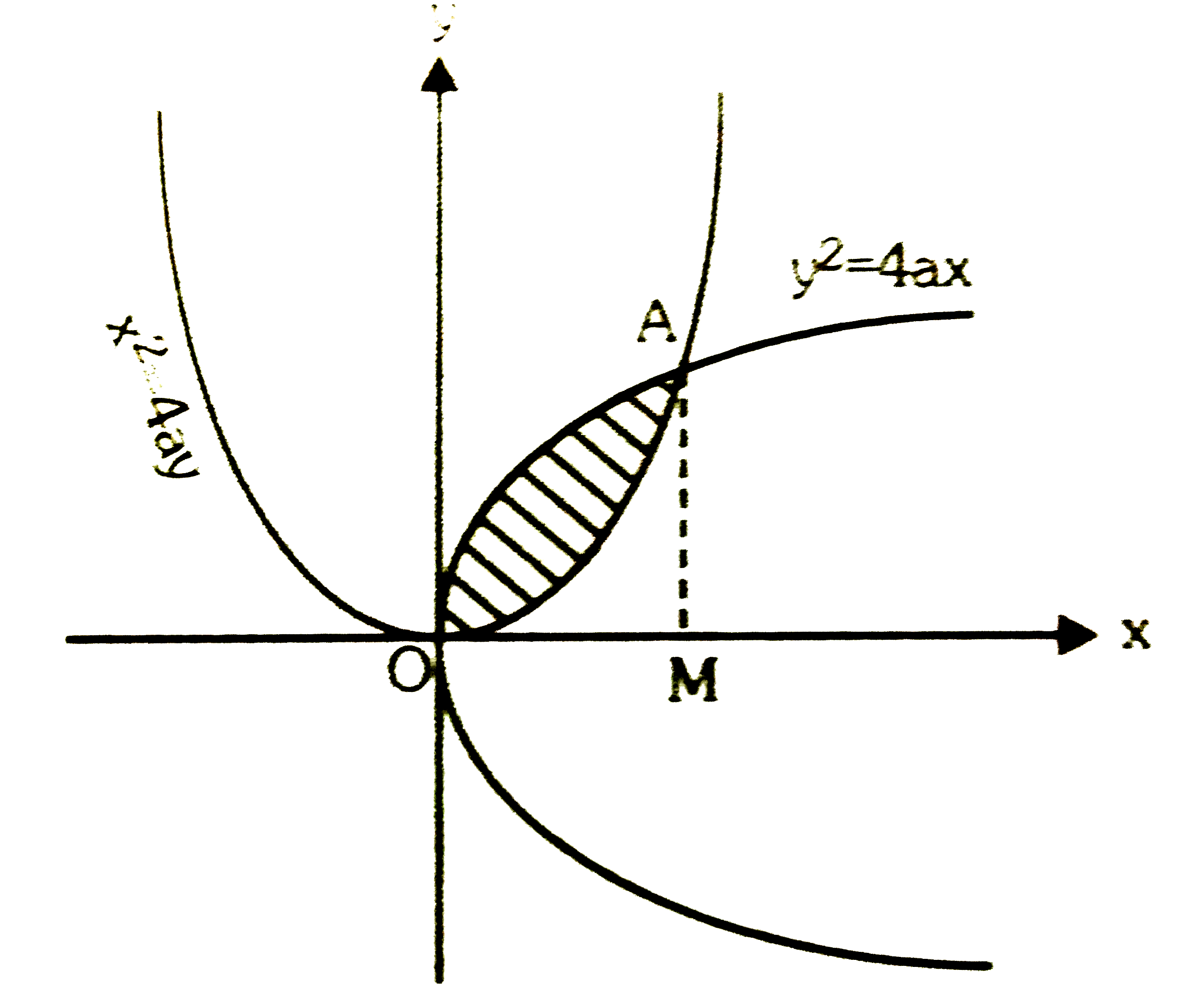
प्रश्नानुसार , हमें छायांकित भाग का क्षेत्रफल ज्ञात करना है | यदि अभीष्ट क्षेत्रफल A है, तब
A=∫4a0ydx [समीकरण (1 ) से] −∫4a0ydx [समीकरण (2 ) से]
=∫4a0√4axdx−∫4a0(x24a)dx
=2a1/2∫4a0x1/2dx−14a∫4a0x2dx
=2a1/2⋅23[x3/2]4a0−14a⋅13[x3]4a0
=4a1/23[(4a)3/2−0]−112a[(4a)3−0]
=4a1/238a3/2−112a64a3
=323a2−163a2=163a2
अतः अभीष्ट क्षेत्रफल = 163a2 वर्ग इकाई
Topper's Solved these Questions
- समाकलन के सरल अनुप्रयोग BOOK - BALAJI PUBLICATIONCHAPTER - समाकलन के सरल अनुप्रयोग EXERCISE - अभ्यास प्रश्न 17.1
12 Videos
- समाकलन के सरल अनुप्रयोग BOOK - BALAJI PUBLICATIONCHAPTER - समाकलन के सरल अनुप्रयोग EXERCISE - अभ्यास प्रश्न 17.2
9 Videos
- समाकलन BOOK - BALAJI PUBLICATIONCHAPTER - समाकलन EXERCISE - स्वमूल्यांकन परीक्षण
24 Videos
- समाकलन क्रमशः BOOK - BALAJI PUBLICATIONCHAPTER - समाकलन क्रमशः EXERCISE - स्वमूल्यांकन परीक्षण
20 Videos
Similar Questions
y=ex,x=0 से x=a तक
View Solutionपरवलय y2=4ax तथा रेखा y=2x द्वारा घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिये |
View Solutionमान ज्ञात कीजिए -∫(4e3x+1)dx
View Solution1x2−9
View Solutionसिद्ध कीजिए कि परवलयो y^(2)=4xतथाx^(2)=4yकेबीचघिरेक्षेत्रफल16/3 वर्ग इकाई का।
View Solutionदिखाइए कि परवलयों y2=4ax तथा x2=4ay के बीच का क्षेत्रफल 163a2 होगा|
View Solutionउस त्रिभुज का क्षेत्रफल ज्ञात कीजिए जिसकी भुजाओ के समीकरणy=ax,y=bx तथा ax+by+c=0 है
View Solutionसिद्ध कीजिए कि बिंदु (1,−6),(5,2),(7,0) तथा (−1,−4)एक चक्रीय चतर्भुज के शीर्ष है ।
View Solutionमाना कि N में एक द्वि - आधारी संकिया ∗, a∗b=a तथा b के LCM द्वारा परिभाषित है , a,b∈N तब सिद्ध कीजिए कि :(20∗16)∗8=20∗(16∗8)
View Solutionवक्र y=logx,x− अक्ष और x = 2 के बीच का क्षेत्रफल है :
View Solutionवक्रों x+2y2=0 तथा x+3y2=1 के बीच घिरे क्षेत्र का क्षेत्रफल है :
View Solutionबिंदुओं (1, 4, 5) तथा (2, 2, 3) के बीच की दुरी कितनी होगी ?
View Solutionसिद्ध कीजिए कि बिन्दु (2,−2),(8,4),(5,7) और (−1,1) एक आयत के शीर्ष है। उसके विकर्णों के बीच का न्यून कोण ज्ञात कीजिए।
View Solutionबिंदुओं (1, 2, 3) तथा (2, 4, 5) के बीच की दूरी ज्ञात कीजिए |
View Solutionरेखा x−2a=y−2b=z−2c तथा समतल ax+by+cz+6=0 के बीच का कोण है -
View Solutionवक्रों y2=2x तथा x2+y2=8 के मध्यवर्ती क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
View Solution
