Question

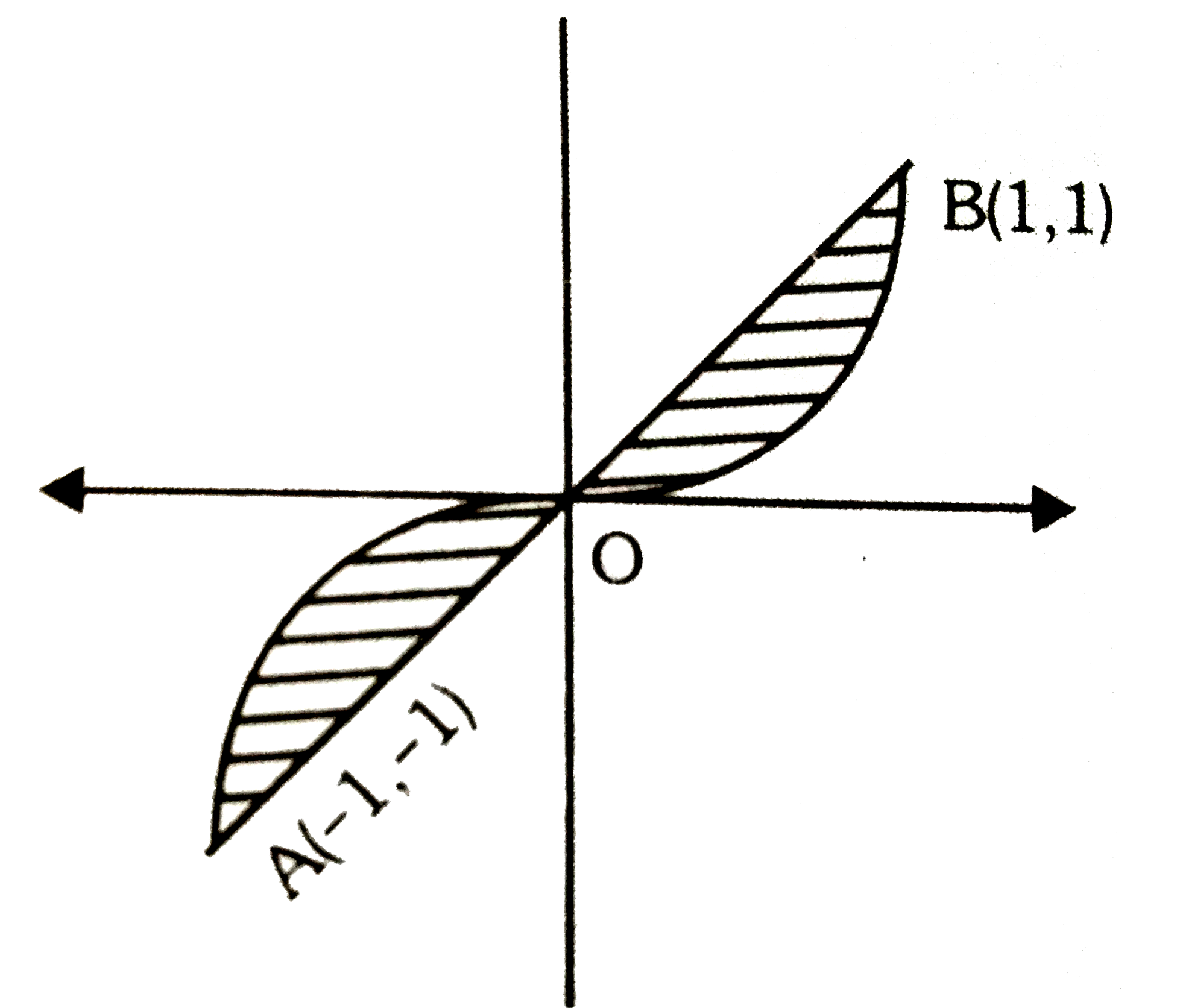
वक्रो $y=x$ तथा $y=x^3$ के मध्य घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए।

Explanation

प्रदत वक्र ` y = x ` ... (1 )
तथा ` y = x ^(3) ` ... (2)
समीकरण (1 ) व (2 ) से,
` x - x ^( 3 ) = 0 `
` x ( 1 - x ) ( 1 + x ) = 0 `
` therefore x = 0, x = 1 `
तथा ` x = - 1 `
समीकरण (1 ) से यदि ` x = 0 " " y = 0`, यदि ` x = 1 ` तब y = 1 तथा यदि ` x = - 1 ` तब ` y = - 1 `
अतः वक्रों (1 ) व (2 ) के प्रतिच्छेद बिंदु
` A ( - 1, - 1 ), O ( 0, 0 ) ` तथा ` B ( 1, 1 ) ` है |
प्रश्नानुसार, हमे छायांकित भाग का क्षेत्रवाल ज्ञात करना है |
हम प्रथम चतुर्थांश में स्थित छायांकित भाग का क्षेत्रफल ज्ञात करके
उस क्षेत्रफल को '2' से गुणा कर देंगे |
हमे अभीष्ट क्षेत्र का क्षेत्रफल ज्ञात हो जाएगा |
प्रथम चतुर्थांश में स्थित क्षेत्र का क्षेत्रफल
` = int _ 0 ^( 1 ) y _ 1 dx - int _ 0 ^( 1 ) y _ 2 dx `
जबकि ` y _ 1 = x ` तथा ` y _ 2 = x ^( 3 ) `
` = int _ 0 ^( 1 ) x dx - int _ 0 ^( 1 ) x ^( 3 ) dx = [ ( x ^( 2 ) ) /( 2 ) ] _ 0 ^( 1 ) - [ ( x ^( 4 ) ) /( 4 ) ] _ 0 ^( 1 ) = ( 1 )/ (2) - ( 1 ) /(4) = (1) /(4) `
अतः अभीष्ट क्षेत्रफल = 2 `xx ` प्रथम चतुर्थांश में स्थित क्षेत्र का क्षेत्रफल
` = 2 xx ( 1 ) /(4) = ( 1 ) /(2) ` वर्ग इकाई