बिन्दु P(2,-1,3) को जाने वाली तथा रेखाओं →r=(ˆi+ˆj+ˆk)+λ(2ˆi−2ˆj+ˆk) तथा →r=(2ˆi−ˆi−3ˆk)+mμ(ˆi+2ˆj+2ˆk) के लंबवत रेखा का समीकरण ज्ञात कीजिए ।
दिया है →r=(ˆi+ˆj+ˆk)+λ(2ˆi−2ˆj+ˆk)
तथा →r=(2ˆi−ˆi−3ˆk)+mμ(ˆi+2ˆj+2ˆk)
ये समीकरण निम्न रूप में लिख सकते है ।
→r=a1=λb1 ...(1)
जहाँ a1=(ˆi+ˆj+ˆk) तथा b1=(2ˆi−2ˆj+ˆk)
→r=a2+λb2 ...(2)
जहाँ a2=(2ˆi−ˆj−3ˆk) तथा b2=(ˆi+2ˆj+ˆk)
अब समीकरण (1) व (1)→b1 के लंबवत रेखा का समीकरण ज्ञात करना है। चूँकि समीकरण (2)→b2 के समान्तर तथा समीकरण (2)→b2 के समान्तर है इसलिए →b1 तथा →b2 लंबवत रेखा ही अभीष्ट रेखा है।
⇒ यह (→b1×→b2) के समान्तर है।
(→b1×→b2)=∣∣
∣
∣∣ˆiˆjˆk2−21122∣∣
∣
∣∣=(−6ˆi−3ˆj+ˆk)
इसलिए हमे बिन्दु P(2,−1,3) से जाने वाली तथा (→b1×→b2) के समान्तर का समीकरण ज्ञात करना है।
इसलिए अभीष्ट रेखा का समीकरण
→r=(2ˆi−ˆj+3ˆk)+K(−7ˆi−3ˆj−6ˆk)
जहाँ K एक स्वैच्छ अचर है।
Topper's Solved these Questions
- त्रिविमीय ज्यामिति : सरल रेखायें एवं समतल BOOK - BALAJI PUBLICATIONCHAPTER - त्रिविमीय ज्यामिति : सरल रेखायें एवं समतल EXERCISE - अभ्यास प्रश्न 22.1
16 Videos
- त्रिविमीय ज्यामिति : सरल रेखायें एवं समतल BOOK - BALAJI PUBLICATIONCHAPTER - त्रिविमीय ज्यामिति : सरल रेखायें एवं समतल EXERCISE - अभ्यास प्रश्न 22.2
21 Videos
- खण्डश: समाकलन BOOK - BALAJI PUBLICATIONCHAPTER - खण्डश: समाकलन EXERCISE - स्वमूल्यांकन परीक्षण
28 Videos
- द्विआधारी संक्रियाएँ BOOK - BALAJI PUBLICATIONCHAPTER - द्विआधारी संक्रियाएँ EXERCISE - स्वमूल्यांकन परीक्षण
11 Videos
Similar Questions
निम्नलिखित सदिशों की दिक् कोज्याये ज्ञात कीजिए-
(i) 2ˆi+2ˆj−ˆk
(ii)6ˆi−2ˆj−3ˆk
View Solutionउस रेखा का समीकाण ज्ञात कीजिए जो बिन्दु (1,2,3) से होकर जाती है तथा रेखा −x−21=y+37=2z−63 के समान्तर है ।
View Solutionx sin x का समाकलन कीजिए-
View Solutionसिद्ध कीजिए की a∗b=a+2b द्वारा प्रदर्शित ⋅:R×R→R क्रमविनिमेय नहीं है|
View SolutionIf vecF=hati+2hatj-3hatk and vecr=2hati-hatj+hatk find vecrxxvecF
View SolutionThe line through ˆi+3ˆj+2ˆk and perpendicular to the lines →r=(ˆi+2ˆj−ˆk)+λ(2ˆi+ˆj+ˆk) and →r=(2ˆi+6ˆj+ˆk)+μ(ˆi+2ˆj+3ˆk) is
View SolutionThe equation of line passing through (3,-1,2) and perpendicular to the lines
→r=(ˆi+ˆj−ˆk)+λ(2ˆi−2ˆj+ˆk)
and →r=(2ˆi+ˆj−3ˆk)+μ(ˆi−2ˆj+2ˆk) is
View SolutionThe lines ¯r=ˆi+2ˆj+3ˆk+λ(ˆi+2ˆj+3ˆk)and¯r=−2ˆj+ˆk+λ(2ˆi+2ˆj−2ˆk) are
View SolutionFind the equation of a line passing through the point P(2,−1,3) and perpendicular to the lines →r=(ˆi+ˆj−ˆk)+λ(2ˆi−2ˆj+ˆk) and →r=(2ˆi−ˆj−3ˆk)+μ(ˆi+2ˆj+2ˆk).
View SolutionFind the angle between the lines →r=ˆi−ˆj+ˆk+λ(2ˆi−2ˆj+ˆk) and →r=2ˆi−ˆj+2ˆk+μ(ˆi+ˆj+2ˆk).
View SolutionA long solenoid having n = 200 turns per metre has a circular cross-section of radius a1=1cm. A circular conducting loop of radius a2=4cm and resistance R=5(Ω) encircles the solenoid such that the centre of circular loop coincides with the midpoint of the axial line of the solenoid and they have the same axis as shown in Fig.
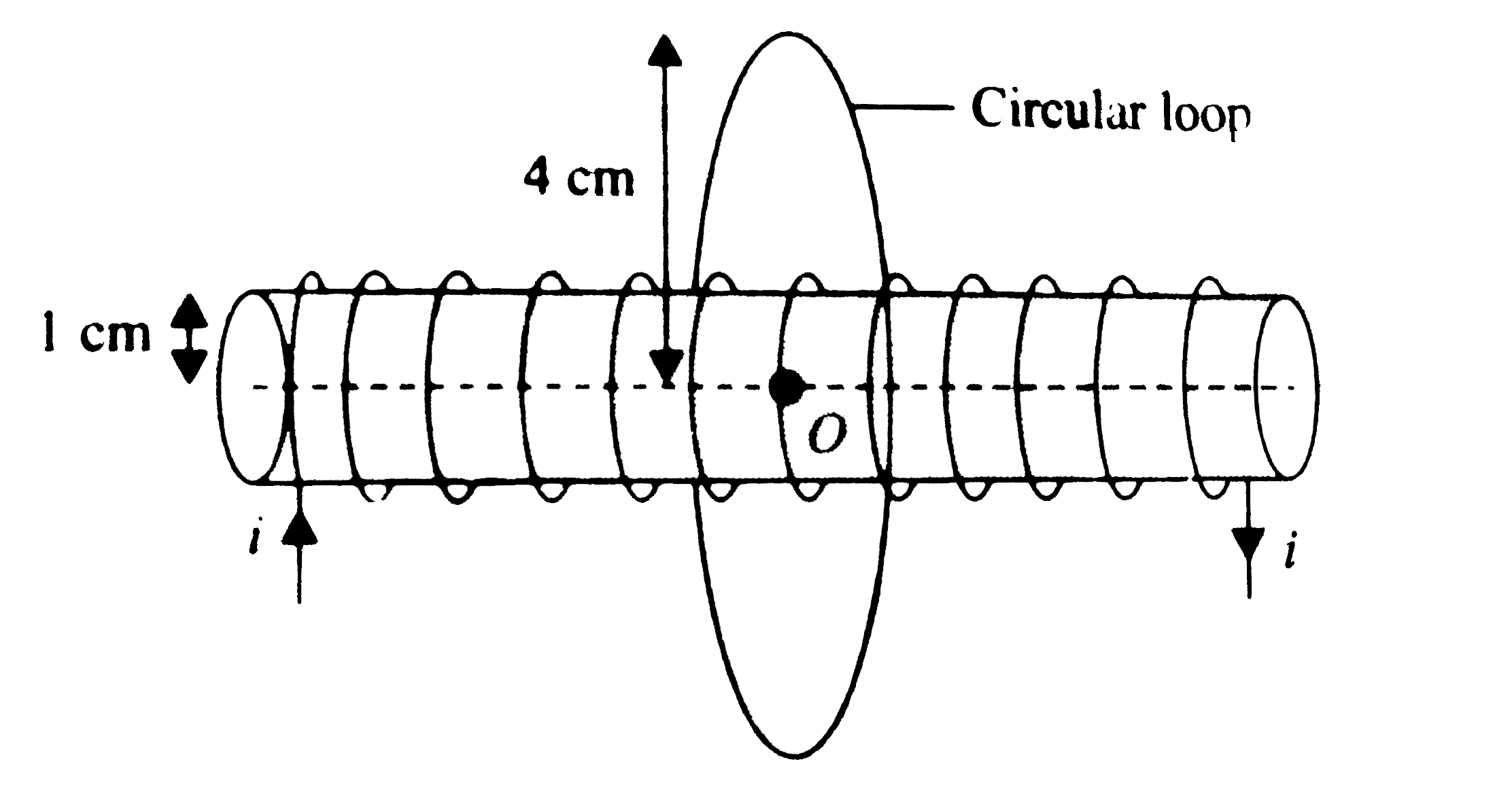
A current 't' in the solenoid results in magnetic field along its axis with magnitude B=(μ)ni at points well inside the solenoid on its axis. We can neglect the insignificant field outside the solenoid. This results in a magnetic flux (ϕ)B through the circular loop. If the current in the winding of solenoid is changed, it will also change the magnetic field B=(μ)0ni and hence also the magnetic flux through the circular loop. Obvisouly, it will result in an induced emf or induced electric field in the circular loop and an induced current will appear in the loop. Let current in the winding of solenoid be reduced at a rate of 75A/sec.
When the current in the solenoid becomes zero so that external magnetic field for the loop stops changing, current in the loop will follow a differenctial equation given by [You may use an approximation that field at all points in the area of loop is the same as at the centre
View SolutionFind the shortest distance between two lines whose vector equations are : →r=ˆi+2ˆj+ˆk+λ(ˆi+ˆj+ˆk) and →r=2ˆi−ˆj−ˆk+μ(2ˆi+ˆj+2ˆk)
View SolutionFind the shortest distance between the lines whose equations are : →r=ˆi+2ˆj+ˆk+λ(ˆi−ˆj+ˆk) and →r=2ˆi−ˆj−ˆk+μ(2ˆi+ˆj+2ˆk).
View SolutionThe lines barr=hati+2hatj+3hatk+lambda(hati+2hatj+3hatk) and barr=-2hatj+hatk+lambda(2hati+2hatj-2hatk) are
View SolutionThe equation of line passing through (3,-1,2) and perpendicular to the lines vecr=(hati+hatj-hatk)+lamda(2hati-2hatj+hatk) and vecr=(2hati+hatj-3hatk) +mu(hati-2hatj+2hatk) is
View Solution
