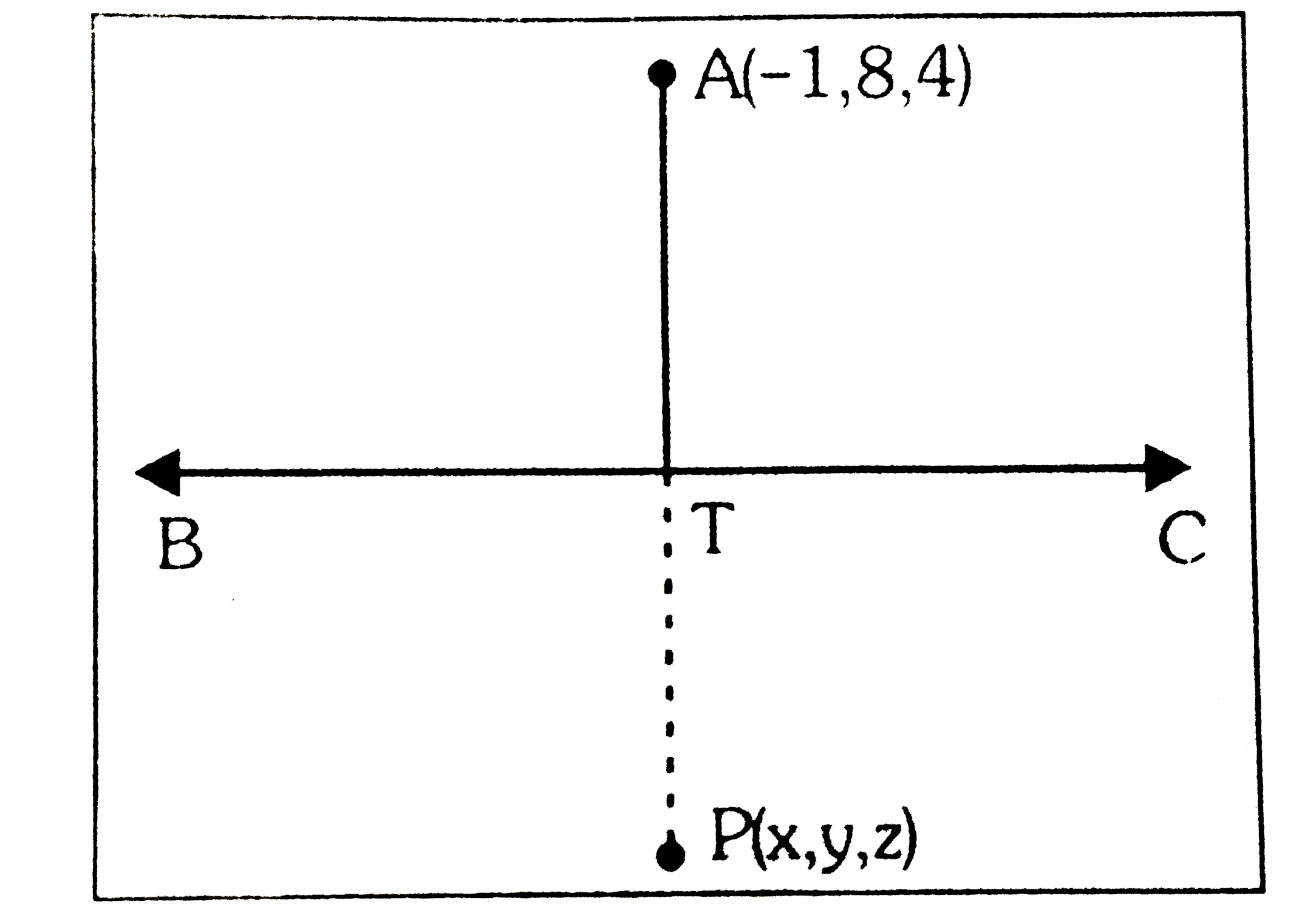
बिन्दु A(1,-8,4) से बिंदुओं B(0,−1,3) तथा C(2,3−1) को मिलाने वाली रेखा पर खींचे गये लंबपाद के निर्देशांक ज्ञात कीजिए । अतएव रेखा BC में बिन्दु A का प्रतिबिम्ब ज्ञात कीजिए ।

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

अब बिंदुओं (0,−1,3) तथा C(2,−3,−1) को मिलाने वाली रेखा की समीकरण
x−02−0=y+1−3+1=z−3−1−3
⇒x2=y+1−2=z−3−4=λ माना
⇒x=2λ,y=−2λ−1,z=−4λ+3
माना बिन्दु A से रेखा BC पर खींचा गया लंबपाद T(2λ,−2λ−1,4λ+3) है।
ocr_image
अब रेखा AT, के दिक् अनुपात
(2λ+1,−2λ−1−8,4λ+3−4)
या (2λ+1,−2λ−9,−4λ−1)
चूँकि AT,BC के लंबवत है-
∴2×(2λ+1)+(−2)×(−2λ−9)+)−4)(−4λ−1)=0
[∴a1a2+b1b2++c1c2=0]
⇒4λ+2+4λ+18+16λ+4=0
A⇒24λ+24=0⇒λ=−1
∴ लंबपाद के निर्देशांक है-
T[2×(−1),−2×(−1)−1,−4×(−1)+3]
या T(−2,17)
माना P बिन्दु BC का रेखा के सापेक्ष प्रतिबिम्ब है।
इसलिए T,AP का मध्य बिन्दु है।
∴T के निर्देशांक =AP के मध्य बिन्दु के निर्देशांक
⇒(−2,1,7)=(x−12,y+82,z+42)
संगत निर्देशांकों की तुलना करने पर-
−2x−12,1=y+82,7z+42
⇒x=−3,y=−6 और z=10
अतः लंबपाद के निर्देशांक T(−2,1,7) है तथा बिन्दु A का प्रतिबिम्ब P(−3,−6,10) है।

Updated on:21/07/2023
|
Class 12MATHSTHREE DIMENSIONAL GEOMETRY

Topper's Solved these Questions

Similar Questions