Figure shows a sector of a circle, centre O, containing an angle θ. Prove that (i) Perimeter of the shaded region is r(tanθ+secθ+πθ180−1) (ii) Area of shaded region is r22(tanθ−πθ180)
tanθ=ABr
AB=rtanθ
secθ=OBOA=OBr
OB=rsecθ
PB=OB−OP=rsecθ−r
arcAB=πrθ180o
Perimeter=rtanθ+rsecθ−r+πrθ1800
=r(tanθ+secθ+πθ180o−1)
Area of ∠OAB=12⋅r2tanθ
Area of shaded region=12r2tanθ−πr2θ360
=r22(tanθ−πθ1800)
Similar Questions
Fig. 15.17, shows a sector of a circle, centre O , containing an angle θo , prove that: (FIGURE) (i) Perimeter of the shaded region is r (tanθ+secθ+πθ180−1) (ii) Area of the shaded region is r22 (tanθ−πθ180)
View SolutionFig. 15.17, shows a sector of a circle, centre O , containing an angle θo , prove that: (FIGURE) (i) Perimeter of the shaded region is r (tanθ+secθ+πθ180−1) (ii) Area of the shaded region is r22 (tanθ−πθ180)
View SolutionFigure shows a sector of a circle of radius r containing an angle θ∘ The area of the sector is Acm2 and the perimeter is 50cm. Prove that θ=360π(25r−1) and A=25r−r2
View SolutionProve that
1secθ−tanθ=secθ+tanθ
View SolutionIn the given figure, is shown a sector OAP of a circle with centre 0, containing ∠θ. AB is perpendicular to the radius OA and meets OP produced at B. Prove that the perimeter of shaded region is r[tanθ+secθ+πθ180−1]
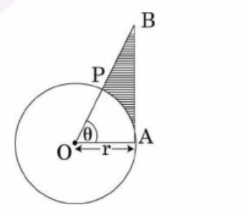
View SolutionIn the given figure, is shown a sector OAP of a circle with centre 0, containing ∠θ. AB is perpendicular to the radius OA and meets OP produced at B. Prove that the perimeter of shaded region is r[tanθ+secθ+πθ180−1]
View SolutionFigure shows a sector of a circle of radius r containing an angle θ∘ The area of the sector is Acm2 and the perimeter is 50cm. Prove that θ=360π(25r−1) and A=25r−r2
View SolutionProve that: 1secθ−tanθ=secθ+tanθ.
View SolutionProve that 1+tan2θtanθ=sec2θ.
View SolutionProve that :
tanθsecθ−1+tanθsecθ+1=2cosecθ
View Solution
