दो वेक्टर →A तथा →B परिणाम में एक-दूसरे के बराबर है तथा दिशा में एक-दूसरे के लंबवत हैं (चित्र) | उचित पैमाना मानकर उनके अग्रलिखित संयोगो को प्रदर्शित कीजिए :
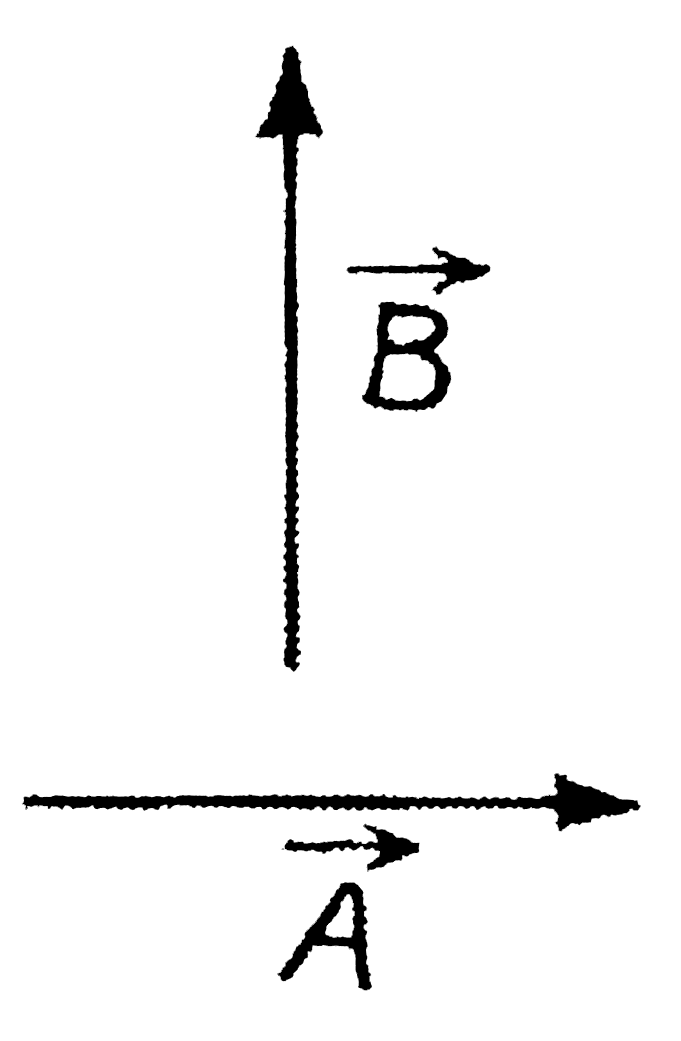
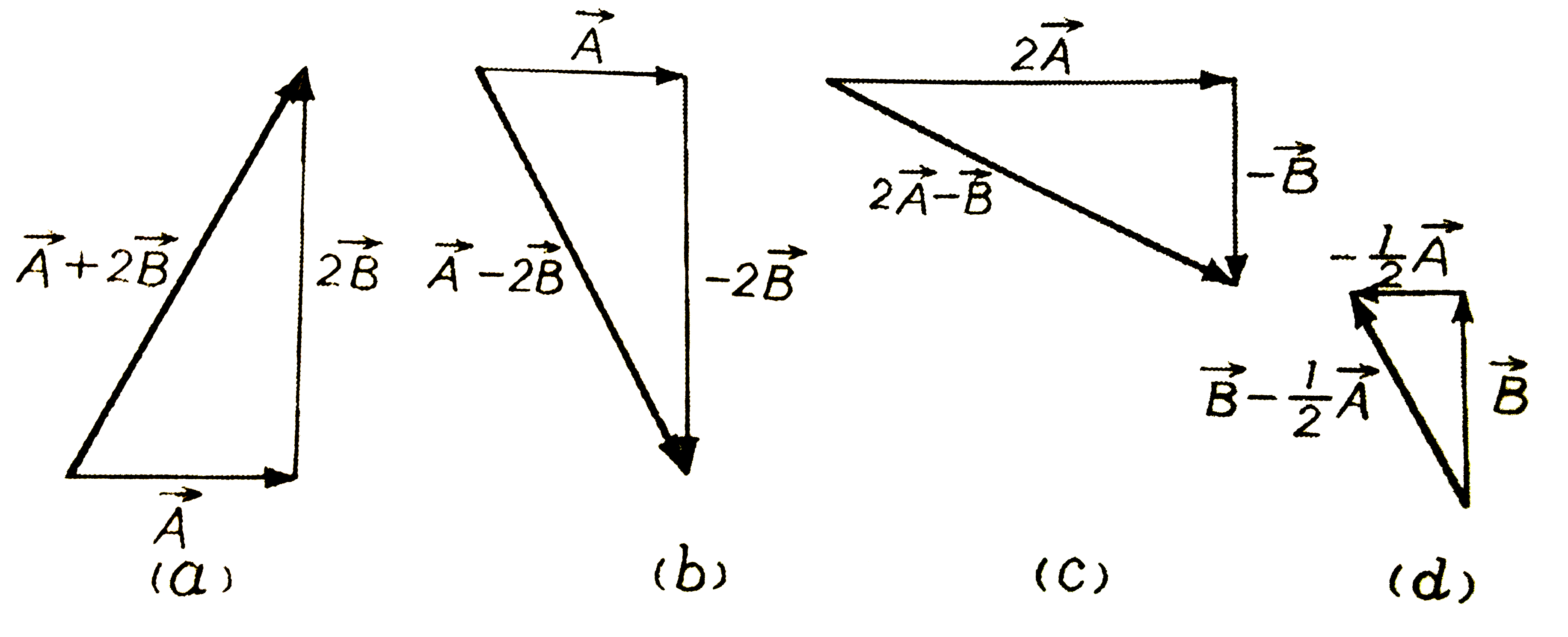
→A+2→B,→A−2→B,2→A−→B,→B−12→A.
दिये गये वेक्टरों →A व →B के विभिन्न संयोग निम्नांकित चित्र (a), (b), तथा (d), में बनाये गये हैं |
Topper's Solved these Questions
- सदिश विश्लेषण एवं प्रक्षेप्य गति BOOK - NOOTAN HINDICHAPTER - सदिश विश्लेषण एवं प्रक्षेप्य गति EXERCISE - प्रश्नावली ( वस्तुनिष्ठ प्रश्न )
30 Videos
- सदिश विश्लेषण एवं प्रक्षेप्य गति BOOK - NOOTAN HINDICHAPTER - सदिश विश्लेषण एवं प्रक्षेप्य गति EXERCISE - अतिलघु उत्तरीय
38 Videos
- वृत्तीय गति BOOK - NOOTAN HINDICHAPTER - वृत्तीय गति EXERCISE - अतिरिक्त प्रशन
17 Videos
- समतापी तथा रुद्धोष्म प्रक्रम BOOK - NOOTAN HINDICHAPTER - समतापी तथा रुद्धोष्म प्रक्रम EXERCISE - वस्तुनिष्ठ प्रकार प्रश्न
17 Videos
Similar Questions
एक बिंदु पर दो बल प्रत्येक 5 न्यूटन के परस्पर 120∘ पर है इन बलों के सदिश योग के परिमाण है :
View Solutionसदिश तथा अदिश राशियों में क्या अंतर है ?
View Solutionचित्र में 0.04 kg सहती के किसी पिंड का स्थिति - समय ग्राफ दर्शाया जय है । इस गति के लिए कोई उचित भौतिक संदर्भ प्रस्तावित कीजिय। पिंड द्वारा प्राप्त दो क्रमिक आवेगों के बिच समय-अंतराल क्या है ? प्रत्येक आवेग का परिमाण क्या है ?

View Solutionकिसी एक परमाण्विक गैस का दाब P और आयतन V है। इसमें पहले समतापीय रूप में 2V आयतन तक और फिर रुद्धोष्म रूप से 16 V आयतन तक प्रसार तक होता है। यदि γ=5/3 हो, तो, गैस का अन्तिम दाब होगा :
View SolutionProve that:(2→a−→b)×(→a+2→b)=5→a×→b.
View SolutionIf →aand→b are unit vectors such that (→a+→b).(2→a+3→b)×(3→a−2→b)=→0 then angle between →aand→b is
View SolutionIf →aand→b are non - zero vectors such that ∣∣→a+→b∣∣=∣∣→a−2→b∣∣ then
View SolutionIf →a,→b are unit vectors such that ∣∣→a+→b∣∣=1and∣∣→a−→b∣∣=√3, " then " ∣∣3→a+2→b∣∣=
View Solutionयदि ∣∣→a+→b∣∣=∣∣→a−→b∣∣ , तब दिखाइये कि सदिश →aतथा →b लम्बवत है |
View Solutionयदि →a.→b=0 तथा →a+→b,→b के साथ 60° का कोण बनाते हैं तो |→a| बराबर है
View Solutionयदि ∣∣→a+→b∣∣=∣∣→b∣∣, तो सिद्ध कीजिए कि →a और →a+2→b परस्पर लम्ब है।
View Solutionसदिशों (→a−→b) और (→c−→b) दोनों के लंबवत एक मात्रक सदिश ज्ञात कीजिए जहाँ →a=ˆi+2ˆj+ˆk,→b=2ˆi+ˆj तथा →c=3ˆi−4ˆj−ˆk.
View Solutionयदि सदिश →a,→b तथा →c के लंबवत है, |→a|=2,∣∣→b∣∣=3,|→c|=4 और →b तथा →c के बिच का कोण 2π3 है। तब [→a→b→c] बराबर है
View Solution[→a+2→b−→c,→a−→b,→a−→b−→c] =
View SolutionIf →aand→b are unit vectors such that (→a+→b).(2→a+3→b)×(3→a−2→b)=→0 then angle between →aand→b is
View SolutionIf →aand→b are non - zero vectors such that ∣∣→a+→b∣∣=∣∣→a−2→b∣∣ then
View Solution
