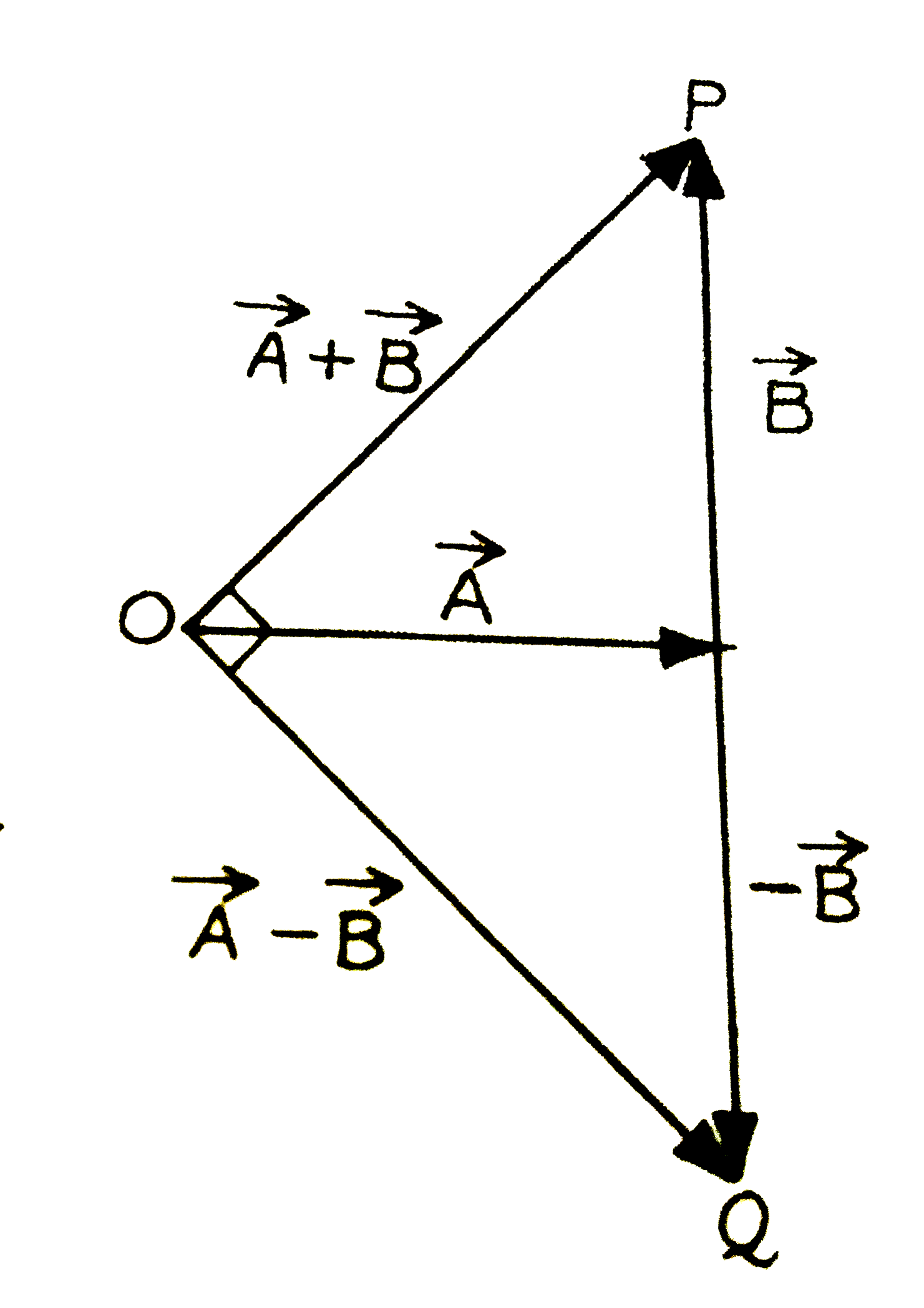
दो सदिश →A एवं →B जिनके परिणाम एकसमान हैं, परस्पर लंबवत हैं | सदिश आरेख बनाकर सिद्ध कीजिए की उनका सदिश योग (→A+→B) तथा सदिश अन्तर (→A−→B) परिणाम में एकसमान तथा परस्पर लंबवत होंगे |
∣∣→A+→B∣∣=√A2+B2
=A√2=B√2
तथा ∣∣→A−→B∣∣=√A2+→B2
=A√2=B√2
अर्थात OP की लम्बाई = OQ की लम्बाई तथा ∠POQ=90∘ .
Topper's Solved these Questions
- सदिश विश्लेषण एवं प्रक्षेप्य गति BOOK - NOOTAN HINDICHAPTER - सदिश विश्लेषण एवं प्रक्षेप्य गति EXERCISE - प्रश्नावली ( वस्तुनिष्ठ प्रश्न )
30 Videos
- सदिश विश्लेषण एवं प्रक्षेप्य गति BOOK - NOOTAN HINDICHAPTER - सदिश विश्लेषण एवं प्रक्षेप्य गति EXERCISE - अतिलघु उत्तरीय
38 Videos
- वृत्तीय गति BOOK - NOOTAN HINDICHAPTER - वृत्तीय गति EXERCISE - अतिरिक्त प्रशन
17 Videos
- समतापी तथा रुद्धोष्म प्रक्रम BOOK - NOOTAN HINDICHAPTER - समतापी तथा रुद्धोष्म प्रक्रम EXERCISE - वस्तुनिष्ठ प्रकार प्रश्न
17 Videos
Similar Questions
एक बिंदु पर दो बल प्रत्येक 5 न्यूटन के परस्पर 120∘ पर है इन बलों के सदिश योग के परिमाण है :
View Solutionसदिश तथा अदिश राशियों में क्या अंतर है ?
View Solutionचित्र में 0.04 kg सहती के किसी पिंड का स्थिति - समय ग्राफ दर्शाया जय है । इस गति के लिए कोई उचित भौतिक संदर्भ प्रस्तावित कीजिय। पिंड द्वारा प्राप्त दो क्रमिक आवेगों के बिच समय-अंतराल क्या है ? प्रत्येक आवेग का परिमाण क्या है ?

View Solutionकिसी एक परमाण्विक गैस का दाब P और आयतन V है। इसमें पहले समतापीय रूप में 2V आयतन तक और फिर रुद्धोष्म रूप से 16 V आयतन तक प्रसार तक होता है। यदि γ=5/3 हो, तो, गैस का अन्तिम दाब होगा :
View Solutionयदि ∣∣→a+→b∣∣=|→a| तो सिद्ध कीजिए की सदिश 2→a+→bसदिश→b पर लम्ब होगा |
View Solutionयदि →a,→b,→c तीन असमतलीय एकांक सदिश है तथा →a×(→c×→b)=→b+→c√2 तो →a और →b के मध्य कोण है -
View Solution→a और →b असंरेख है |यदि सदिश →α=(x−2)→a+→b और →β=(3+2x)→a−2→b संरेख सदिश हो तो x का मान ज्ञात कीजिए|
View Solutionयदि →a और →b असंरेख है ,तो x का मान ज्ञात कीजिए| जिसके लिए सदिश α=(2x+1)→a−→b और β=(x−2)→a+→b संरेख है
View Solutionयदि →a,→b,→c तीन सदिश इस प्रकार हैं कि →a.→b=→a.→c,→a×→b=→a×→c तथा →a≠0 तो दिखाइए कि →b=→c.
View Solution→a,→b,→c क्रमश 3,4,5 परिमाण के सदिश है। यदि प्रत्येक सदिश अन्य दो सदिशो के योग पर लम्ब हो, तो सदिश →a+→b+→c का परिमाण ज्ञात किजिए।
View Solutionयदि दो सदिश →a और →b इस प्रकार है कि |→a|=2,∣∣→b∣∣=3 और →a⋅→b=4 तो ∣∣→a−→b∣∣ ज्ञात किजिए।
View Solutionसदिश →a=ˆi+2ˆj−3ˆk तथा →b=3ˆi−ˆj+2ˆk दोनो के लम्बवत एक एसा सदिश ज्ञात किजिए, जिसका परिमाण √171 हो।
View Solutionयदि →a,→b,→c समान परिमाण के परस्पर लम्ब सदिश हो तो सिद्ध कीजिए कि सदिश →a+→b+→c सदिशों →a,→b और →c के साथ बराबर कोण बनाता है।
View Solutionयदि ∣∣→a+→b∣∣=∣∣→b∣∣, तो सिद्ध कीजिए कि →a और →a+2→b परस्पर लम्ब है।
View Solutionयदि →a,→b तथा →c समबाहु त्रिभुज के शीर्ष के स्थिति सदिश हो जिसका लम्ब केंद्र मूलबिंदु है , तो →a+→b+→c का मान ज्ञात कीजिए।
View Solutionसदिशों (→a−→b) और (→c−→b) दोनों के लंबवत एक मात्रक सदिश ज्ञात कीजिए जहाँ →a=ˆi+2ˆj+ˆk,→b=2ˆi+ˆj तथा →c=3ˆi−4ˆj−ˆk.
View Solution
