(i) क्या यह सम्भव हैं कि समान परिणाम के दो सदिशों के योग को परिणाम भी दिये गये प्रत्येक सदिश के परिणाम के बराबर हो ? (ii) दिये गये सदिशों के अन्तर का परिणाम प्रत्येक सदिश के परिणाम के सापेक्ष कितना होगा ?

Video Solution

Text Solution

Verified by Experts

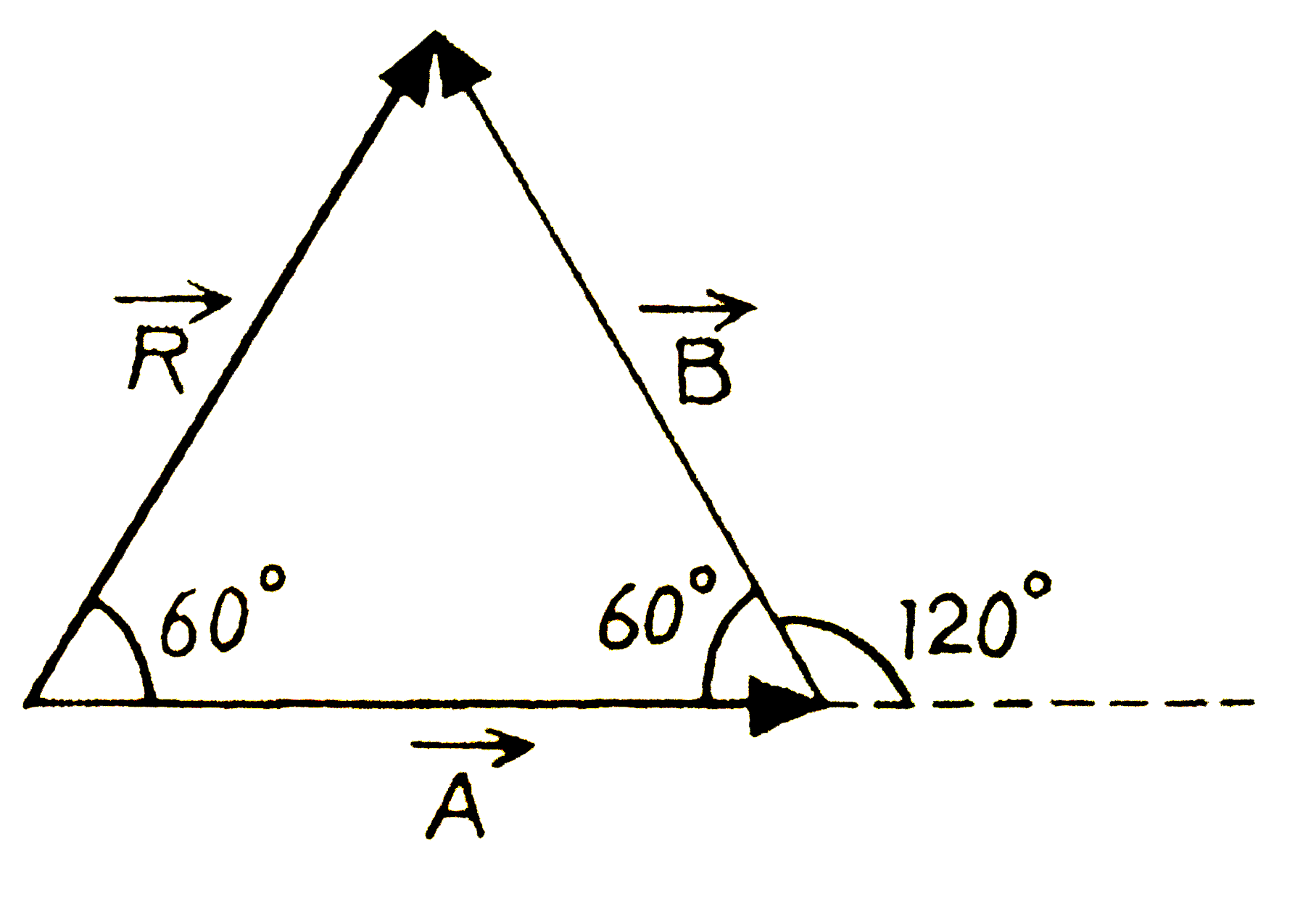
(i) दो सदिशों ( जो किसी कोण पर झुके हों ) तथा उनके योग-सदिश से मिलकर सदैव एक त्रिभुज बनता हैं | यदि ये तीनों ही परिणाम में बराबर हैं, तो त्रिभुज समबाहु त्रिभुज होगा जिनका प्रत्येक कोण $60^{\circ}$ होता हैं चित्र में $\to A$ तथा $\to B$ दो सदिश हैं | $(A = B)$ जिनका योग-सदिश $\to R$ हैं, जबकि $R = A = B$ . इस प्रकार, समान परिणाम के सदिशो $\to A$ तथा $\to B$ का प्रणामी सदिश $\to B$ भी उसी परिणाम का हैं | | इस दशा में दिये गये सदिशों $\to A$ तथा $\to B$ के बीच का कोण $120^{\circ}$ होना चाहिये |
वैकल्पिक विधि: माना दो सदिश $\to A$ तथा $\to B$ हैं, जहाँ $A = B$
इनका योग $\to R = \to A + \to B$
दोनों ओर स्वतः अदिश घुँण करने पर
$\to R \cdot \to R = (\to A + \to B) \cdot (\to A + \to B) = \to A \cdot \to A + 2 \to A \cdot \to B + \to B \cdot \to B$
अथवा $R^{2} = A^{2} + 2 A B cos θ + B^{2}$
जहाँ $θ$ सदिशों $\to A$ तथा $\to B$ के बीच कोण हैं |
यदि $R = A = B$ हों, तब समीकरण से,
$A^{2} = A^{2} + 2 A^{2} cos θ + A^{2}$
अथवा $2 {\to A}^{2} cos θ = - A^{2}$
अथवा $cos θ = - \frac{1}{2}$
अथवा $θ = 120^{\circ}$ .
इस दशा में दिये गये सदिशों के बीच कोण $120^{\circ}$ होना चाहिये |
(ii) अब, माना दिये गये सदिशों का अन्तर $\to R'$ हैं, अर्थात
$\to R' = \to A - \to B$
पुनः स्वतः अदिश गुणन करने पर
$R^{2} = A^{2} - 2 A B cos θ + B^{2}$ .
प्रश्नानुशार, $B = A$ तथा $cos θ = - 1 / 2$ .
$∴ R^{2} = A^{2} + A^{2} + A^{2} = 3 A^{2}$
अथवा $R' = \sqrt{3} A$ .
दिये गये सदिशों के अन्तर का परिणाम प्रत्येक के परिणाम का $\sqrt{3}$ गुना होगा |

|

Updated on:21/07/2023

Class 11 PHYSICS PROJECTILE MOTION

Topper's Solved these Questions

Similar Questions

NOOTAN HINDI-सदिश विश्लेषण एवं प्रक्षेप्य गति -अतिरिक्त प्रश्न

Home
Ask Doubt
Profile