सिद्ध कीजिए कि किसी त्रिभुज के लिए, sinαA=sinβB=sinγc, जहाँ →A,→B तथा →C क्रमशः कोण α,β तथा γ के सम्मुख त्रिभुज की भुजायें है |
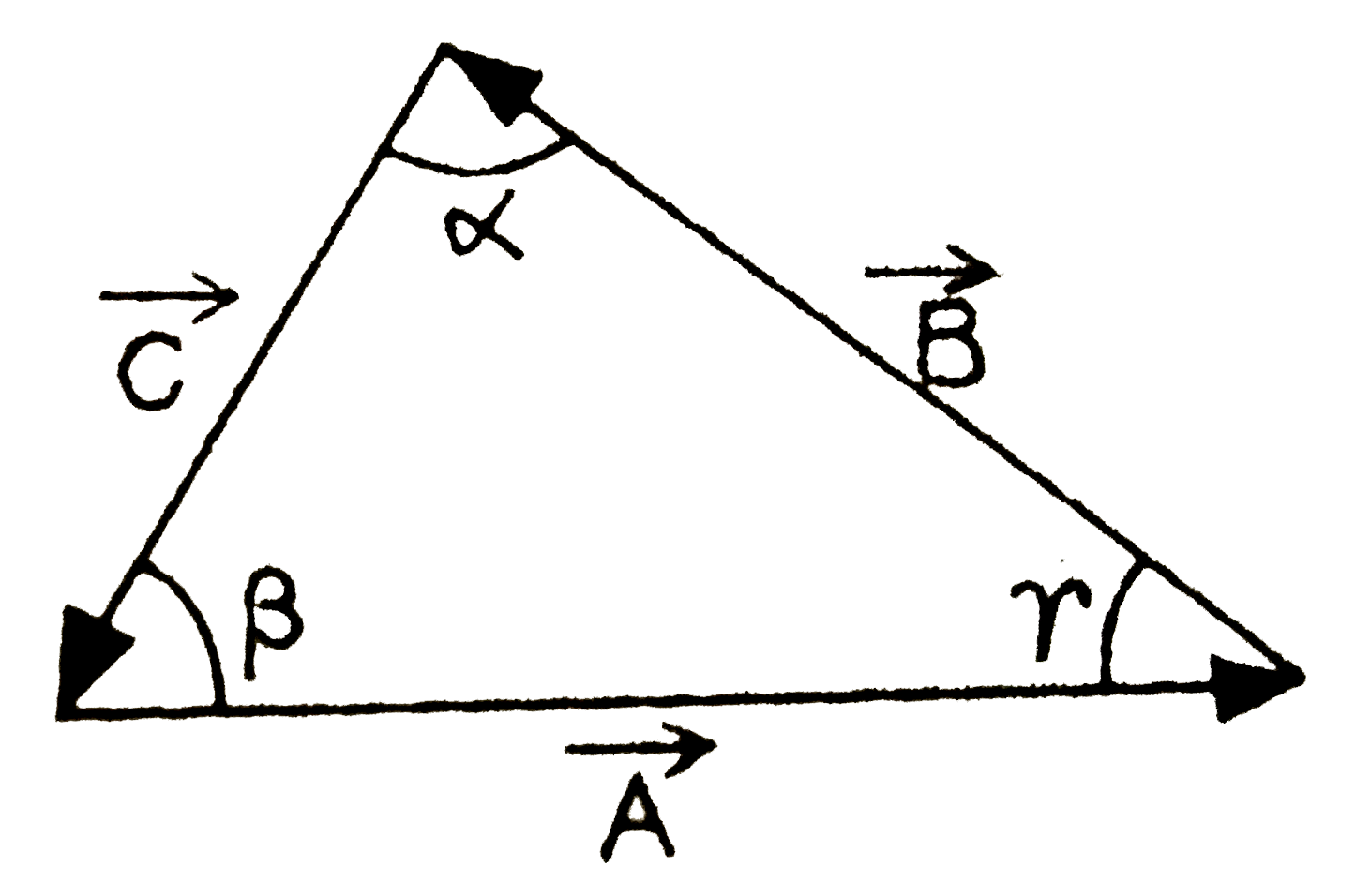
माना →A,→B तथा →C एक त्रिभुज की तीन भुजाओं को प्रदर्शित करते है तथा α,β व γ क्रमशः →A,→B व →C के सम्मुख कोण है ( चित्र ) | सदिश योग के नियमानुसार,
→A+→B+→C=0 …(i)
→B के साथ सदिश गुणनफल लेने पर,
→A×→B+→B×→B+→C×→B=0
अथवा →A×→B+→C×→B=0 [∴→B×→B=0]
अथवा →A×→B=−→C×→B=→B×→C. ...(ii)
अब समीकरण (i) का के साथ सदिश गुणनफल लेने पर,
→A×→C+→B×→C+→C×→C=0
अथवा →A×→C+→B×→C=0 [∴→C×→C=0]
अथवा →B×→C=−→A×→C=→C×→A. ....(iii)
समीकरण (ii) तथा (iii) की तुलना करने पर,
→B×→C=→C×→A=→A×→B
अथवा ∣∣→B×→C∣∣=∣∣→C×→A∣∣=∣∣→A×→B∣∣.
अथवा BCsinα=CAsinβ=ABsinγ
ABC से भाग देने पर, sinαA=sinβB=sinγC
Topper's Solved these Questions
- सदिश विश्लेषण एवं प्रक्षेप्य गति BOOK - NOOTAN HINDICHAPTER - सदिश विश्लेषण एवं प्रक्षेप्य गति EXERCISE - प्रश्नावली ( वस्तुनिष्ठ प्रश्न )
30 Videos
- सदिश विश्लेषण एवं प्रक्षेप्य गति BOOK - NOOTAN HINDICHAPTER - सदिश विश्लेषण एवं प्रक्षेप्य गति EXERCISE - अतिलघु उत्तरीय
38 Videos
- वृत्तीय गति BOOK - NOOTAN HINDICHAPTER - वृत्तीय गति EXERCISE - अतिरिक्त प्रशन
17 Videos
- समतापी तथा रुद्धोष्म प्रक्रम BOOK - NOOTAN HINDICHAPTER - समतापी तथा रुद्धोष्म प्रक्रम EXERCISE - वस्तुनिष्ठ प्रकार प्रश्न
17 Videos
Similar Questions
एक बिंदु पर दो बल प्रत्येक 5 न्यूटन के परस्पर 120∘ पर है इन बलों के सदिश योग के परिमाण है :
View Solutionसदिश तथा अदिश राशियों में क्या अंतर है ?
View Solutionचित्र में 0.04 kg सहती के किसी पिंड का स्थिति - समय ग्राफ दर्शाया जय है । इस गति के लिए कोई उचित भौतिक संदर्भ प्रस्तावित कीजिय। पिंड द्वारा प्राप्त दो क्रमिक आवेगों के बिच समय-अंतराल क्या है ? प्रत्येक आवेग का परिमाण क्या है ?

View Solutionकिसी एक परमाण्विक गैस का दाब P और आयतन V है। इसमें पहले समतापीय रूप में 2V आयतन तक और फिर रुद्धोष्म रूप से 16 V आयतन तक प्रसार तक होता है। यदि γ=5/3 हो, तो, गैस का अन्तिम दाब होगा :
View Solutioncos alpha sin (beta-gamma) + cos beta sin (gamma-alpha) + cos gamma sin (alpha-beta) =
View SolutionLet alpha,beta and gamma are the angles of a right angle triangle,then the value of sin alpha*sin beta*sin(alpha-beta)+sin beta*sin gamma*sin(beta-gamma)+sin gamma*sin alpha*sin(gamma-beta)+sin(beta-gamma)*sin(gamma-gamma)*sin(gamma-
View SolutionProve that : sinα+sinβ+sinγ−sin(α+β+γ)=4sin(α+β2).sin(β+γ2).sin(γ+α2)
View Solutionकिसी ΔABC में सिध्द कीजिये कि:
यदि α=β+γ तो सिध्द कीजिये कि :
sin(α+β+γ)+sin(α+β−γ)+sin(α−β+γ)=4sinαcosβcosγ
View SolutionIf cosα+cosβ+cosγ=0
=sinα+sinβ+sinγ then show that
sin3α+sin3β+sin3γ=3sin(α+β+γ)
View Solutioncosαsin(β−γ)+cosβsin(γ−α)+cosγsin(α−β)=
View Solutionकिसी त्रिभुज कि भुजाओ के मध्य बिन्दुओ के निर्देशांक क्रमशः (2,1),(−5,7) तथा (−5,5) है त्रिभुज कि भुजाओ के समीकरण ज्ञात कीजिए ।
View Solutionसिद्ध करें की sinα⋅sin(β−γ)+sinβ⋅sin(γ−α)+sinγ⋅sin(α−β)=0
View Solutionsin (beta+ gamma- alpha) + sin (gamma+ alpha - beta) + sin (alpha + beta- gamma)- sin (alpha + beta + gamma)=
View Solutioncosα⋅sin(β−γ)+cosβ⋅sin(γ−α)+cosγ⋅sin(α−β)=
View SolutionProve that : sinα+sinβ+sinγ−sin(α+β+γ)<br>=4sinα+β2sinβ+γ2sinγ+α2
View Solution
