Question

समुच्चय $\{1,2,3,4,5\}$ में , निम्नलिखित संक्रिया सारणी (सारणी 1.1) द्वारा परिभाषित द्विआधारी संक्रिया $\ast$ पर विचार कीजिए तथा
(i) $(2\ast 3)\ast 4$ तथा $2\ast (3\ast 4)$ का परिकलन कीजिए ।
(ii) क्या $\ast$ क्रमविनिमेय है ?
(iii) $(2\ast 3)\ast (4\ast 5)$का परिकलन कीजिए ।
( संकेत : निम्न सारणी का प्रयोग कीजिए ।)
सारणी 1.1

Explanation

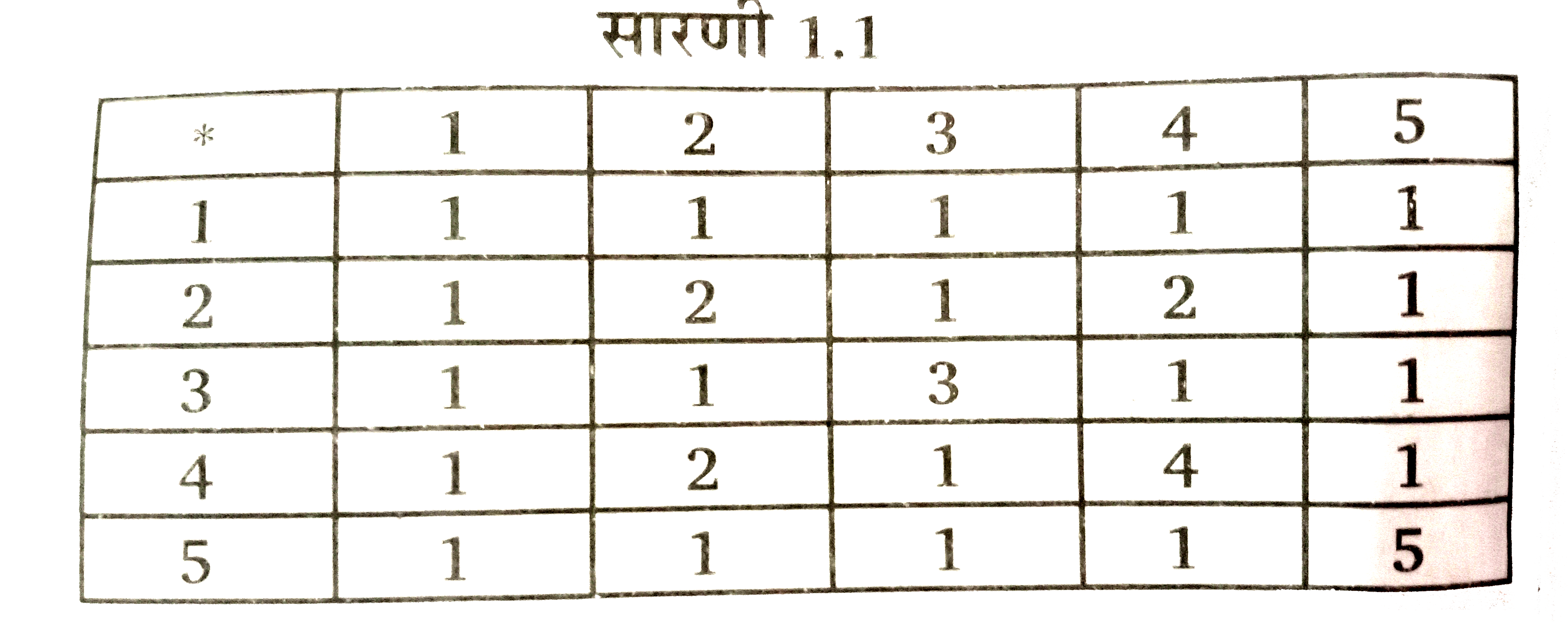
(i) `(2**3)**4=1**4=1`
तथा `2**(3**4)=2**1=1`
(ii) `:'` प्रत्येक `a,b in {1,2,3,4,5}` के लिये
`a**b=b**a`
`:.**` क्रमविनिमेय है।
`(iii) (2**3)**(4**5)=1**1=1`