ax+by=c bx+ay=1+c
रेखिक समीकरणो के युग्मो को हल कीजिए :
ax+by=c ⇒ax+by−c=0
⇒ bx+ay=1+c ⇒bx+ay−(1+c)=0
अब 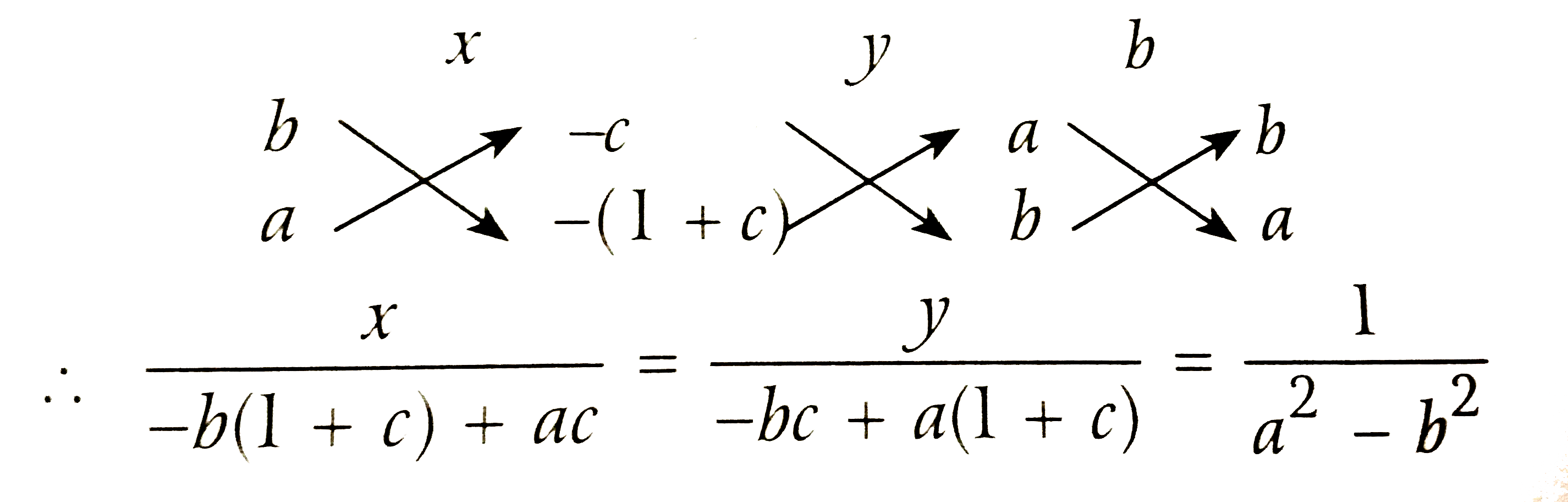
∴x−b(1+c)+ac=y−bc+a(1+c)=1a2−b2
⇒xac−b−bc=1a2−b2
और y−bc+a+ac=1a2−b2
⇒ x=ac−b−bca2−b2
और y=a+ac−bca2−b2
Topper's Solved these Questions
- दो चर वाले रैखिक समीकरण युग्म Book:NOOTAN HINDIChapter:दो चर वाले रैखिक समीकरण युग्म Exercise:विविध प्रश्नावली ( अतिलघु उत्तरीय प्रश्न )
Explore 9 Videos
- दो चर वाले रैखिक समीकरण युग्म Book:NOOTAN HINDIChapter:दो चर वाले रैखिक समीकरण युग्म Exercise:विविध प्रश्नावली (लघु उत्तरीय प्रश्न)
Explore 10 Videos
- दो चर वाले रैखिक समीकरण युग्म Book:NOOTAN HINDIChapter:दो चर वाले रैखिक समीकरण युग्म Exercise:एन०सी०ई०आर०टी० प्रश्न (प्रश्नावली 3.6)
Explore 11 Videos
- त्रिभुज Book:NOOTAN HINDIChapter:त्रिभुज Exercise:विविध प्रश्नावली (बहु विकल्पीय प्रश्न)
Explore 7 Videos
- द्विघात समीकरण Book:NOOTAN HINDIChapter:द्विघात समीकरण Exercise:विविध प्रश्नावली (बहुविकल्पीय प्रश्न)
Explore 7 Videos
Similar Questions
k के किस मान के लिए दो युगपत समीकरणो x+y=2 और x−by=1 का कोई हल नहीं होगा ?
View Solutionहल कीजिए: 3x+2y=11 और 2x+2y=4
View Solutionनिम्न समीकरणो के युग्मो को रेखिक समीकरणो के युग्म में बदल करके हल कीजिए :
12x+13y=2 13x+12y=136
View Solutionएक समचतुर्भुज के विकर्णो की लम्बाई 16cm और 12cm है इसकी भुजा की लम्बाई है :
View Solutionनिम्नलिखित प्रश्न में चार विकल्प दिए गए हैं। उस विकल्प को चुनकर अपनी उत्तर पुस्तिका में लिखिए जिसके मूल वास्तविक हैं:
View SolutionSolve: ax+by=c, bx+ay=1+c
View Solutionनिम्नलिखित समीकरणों को हल कीजिए : ax+by=c,bx+ay=1+c.
View Solutionनिम्नलिखित समीकरण निकाय को हल करें-
ax+by=c,bx+ay=1+c
View Solutionनिम्न समीकरण युग्म को हल करो :
ax+by=c
bx+ay=1+c
View Solutionनिम्न समीकरण युग्म को हल करो :
ax+by=c
bx+ay=1+c
View Solutionत्रिकोणमितीय समीकरणो के व्यापक हल
View SolutionThe equation of a line perpendicular to line ax+by+c=0 and passing through (a,b) is equal to ................ A) bx−ay=0 B) bx+ay−2ab=0 C) bx+ay=0 D) bx−ay+2ab=0
View Solutionनिम्न समीकरणों के निकाय को हल कीजिए :
ax + by = c
bx + ay = 1 + c
View Solutionगुणनखंडन कीजिए-
ax+ay−bx−by
View Solutionਹੇਠਾਂ ਦਿੱਤੇ ਸਮੀਕਰਣ ਜੋੜਿਆਂ ਨੂੰ ਹੱਲ ਕਰੋ : ax+by=c, bx+ay=1+c
View Solution