दर्शाइए कि एक विषम धनात्मक पूर्णांक का वर्ग किसी पूर्णांक q के लिए 8k + 1 के रूप का होता है ।
माना n एक विषम धनात्मक पूर्णांक है, इसलिए n2 भी एक विषम धनात्मक पूर्णक होगा ।
तब n, 8q + 1, 8q + 3, 8q + 5 तथा 8q + 7 में से किसी एक रूप का होगा ।
जब n = 8q + 1
⇒ n2=(8q+1)2=64q2+16q+1
=8(8q2+2q)+18k+1 जहाँ k=8q2+2q
यदि n = 8q + 3
⇒ n2=(8q+3)2=64q2+48q+9
=8(8q2+6q+1)+1=8k+1 जहाँ k=8q2+6q+1
यदि n = 8q + 5
⇒ n2=(8q+5)2=64q2+80q+25
=8(8q2+10q+3)+1=8k+1 जहाँ k=8q2+10q+3
यदि n = 8q + 7
⇒ n2=(8q+7)2=64q2+112q+49
=8(8q2+14q+6)+1=8k+1 जहाँ k=8q2+14q+6
उपरोक्त से स्पष्ट है की सभी स्थितियों में n2, किसी पूर्णांक k के लिए 8k + 1 के रूप का है ।
Topper's Solved these Questions
- वास्तविक संख्याऐंBook:BALAJI PUBLICATIONChapter:वास्तविक संख्याऐंExercise:विविध उदाहरण
Explore 9 Videos
- वास्तविक संख्याऐंBook:BALAJI PUBLICATIONChapter:वास्तविक संख्याऐंExercise:अतिलघु उत्तरीय प्रश्न
Explore 24 Videos
- रचनाऐBook:BALAJI PUBLICATIONChapter:रचनाऐExercise:स्वमूल्यांकन परिक्षण
Explore 2 Videos
- वृत्त Book:BALAJI PUBLICATIONChapter:वृत्त Exercise:स्वमूल्यांकन परीक्षण
Explore 15 Videos
Similar Questions
पूर्णांक a व 3 के लिए, अद्वितीय पूर्णांक q व r का अस्तित्व इस प्रकार है की a = 3q + r, तब r के संभावित मान ज्ञात कीजिए ।
View Solution1152 व 1664 को पूर्णतया विभाजित करने वाली सबसे बड़ी संख्या ज्ञात कीजिए ।
View Solution5.6 सेमी का रेखाखण्ड खींचकर उसे 5:8 के अनुपात में अन्तः विभक्त कीजिए
View Solutionदिये गये चित्र में TAB, O केंद्र वाले वृत्त की छेदक रेखा है तथा वृत्त के बिन्दु P पर TP एक स्पर्शी है। यदि TP = 5.6 सेमी तथा TA = 2.8 सेमी हो तब जीवा AB की माप ज्ञात कीजिए ।
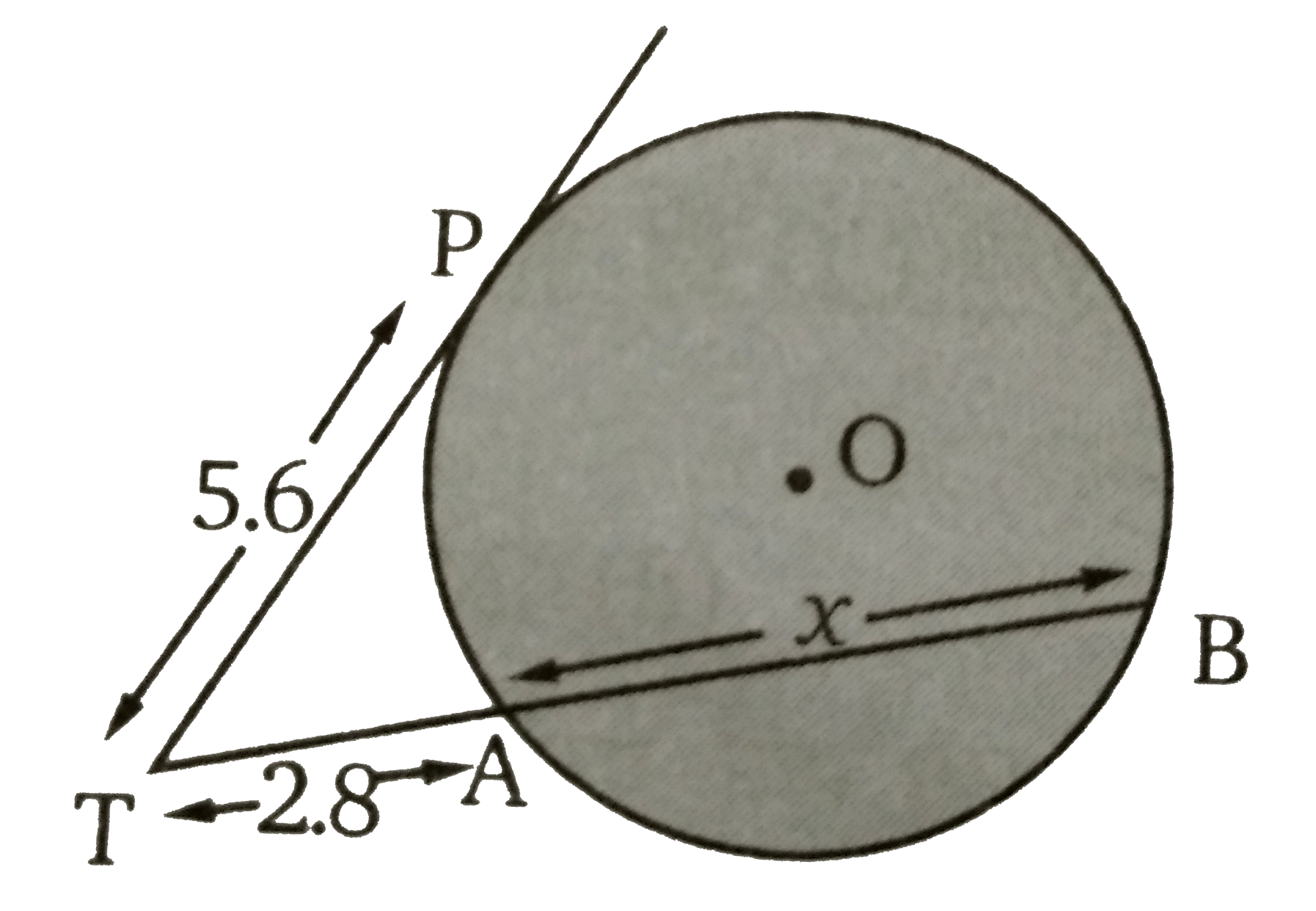
View Solutionसममित तथा विषम सममित आव्यूह | किसी वर्ग आव्यूह का एक सममित तथा एक विषम सममित आव्यूह के योगफल के रूप में निरूपण | उदाहरण
View Solutionm के उन पूर्णांक मानो, जिनके लिए द्विपद व्यंजक (1+2m)x2−2(1+3m)x+4(1+m),x∈R सदैव धनात्मक है, की संख्या है
View Solutionमाना m ऐसा न्यूनतम धनात्मक पूर्णांक है की (1+x)2+(1+x)3+........+(1+x)49+(1+xm)50 के विस्तार में x2 का गुणांक (3n+1)51C3 किसी धनात्मक पूर्णांक n के लिए तब, n का मान है
View Solutionm के पूर्णांक मानों की संख्या, जिसके लिए रेखाओं 3x +4y= 9 तथा y=mx + 1 के प्रतिच्छेद बिन्दु का x-निर्देशांक भी पूर्णांक हो, है
View Solutionद्विपद प्रमेय किसी धन पूर्णांक n के लिए | महत्वपूर्ण प्रेक्षण | उदाहरण
View Solutionकिसी वर्ग के अंतराल 140-170 का वर्ग चिन्ह होगा :
View Solutionदर्शाइए कि धनात्मक सम पूर्णांक 4q या 4q+2 के रूप का होता है, जहाँ एक पूर्णाक है।
View Solutionपूर्णांक #!#पूर्णांकों का गुणन
View Solutionपूर्णांक#!#पूर्णांक के गुणन के गुण
View Solutionपूर्णांक #!#पूर्णांकों का विभाजन
View Solutionकिसी भी पूर्णांक घात के लिए द्विपद प्रमेय #!#उदाहरण
View Solutionवैधुत क्षेत्र क्या होता है#!#एक बिंदु आवेश के लिए वैधुत क्षेत्र का सूत्र व प्रशन
View Solution