सिध्द कीजिए की यदि p एक अभाज्य संख्या है तो √p एक अपरिमेय संख्या है ।
यहाँ p एक अभाज्य संख्या है । यदि सम्भव हो तो √p एक अपरिमेय संख्या नहीं है तब √p एक परिमेय संख्या होगी । तब दो सहअभाज्य संख्याऐं p व q का अस्तित्व इस प्रकार है की
√p=mn ⇒ p=m2n2 ⇒ pn2=m2
⇒p,m2 को विभाजित करता है । अत: p, m को विभाजित करता है । ...(1)
माना m = pq, किसी पूर्णांक q के लिए
तब pn2=m2 ⇒ pn2=p2q2 ⇒ n2=pq2
⇒p,n2 को विभाजित करता है । अत: p, n को विभाजित करता है । ...(2)
समीकरण (1) व (2) से निष्कर्षत: p, m व n में एक उभयनिष्ट गुणनखण्ड है जोकि सम्भव नहीं है । अत: हमारी कल्पना गलत है इसलिए √p एक अपरिमेय संख्या है ।
Topper's Solved these Questions
- वास्तविक संख्याऐंBOOK - BALAJI PUBLICATIONCHAPTER - वास्तविक संख्याऐंEXERCISE - विविध उदाहरण
9 Videos
- वास्तविक संख्याऐंBOOK - BALAJI PUBLICATIONCHAPTER - वास्तविक संख्याऐंEXERCISE - अतिलघु उत्तरीय प्रश्न
24 Videos
- रचनाऐBOOK - BALAJI PUBLICATIONCHAPTER - रचनाऐEXERCISE - स्वमूल्यांकन परिक्षण
2 Videos
- वृत्त BOOK - BALAJI PUBLICATIONCHAPTER - वृत्त EXERCISE - स्वमूल्यांकन परीक्षण
15 Videos
Similar Questions
पूर्णांक a व 3 के लिए, अद्वितीय पूर्णांक q व r का अस्तित्व इस प्रकार है की a = 3q + r, तब r के संभावित मान ज्ञात कीजिए ।
View Solution1152 व 1664 को पूर्णतया विभाजित करने वाली सबसे बड़ी संख्या ज्ञात कीजिए ।
View Solution5.6 सेमी का रेखाखण्ड खींचकर उसे 5:8 के अनुपात में अन्तः विभक्त कीजिए
View Solutionदिये गये चित्र में TAB, O केंद्र वाले वृत्त की छेदक रेखा है तथा वृत्त के बिन्दु P पर TP एक स्पर्शी है। यदि TP = 5.6 सेमी तथा TA = 2.8 सेमी हो तब जीवा AB की माप ज्ञात कीजिए ।
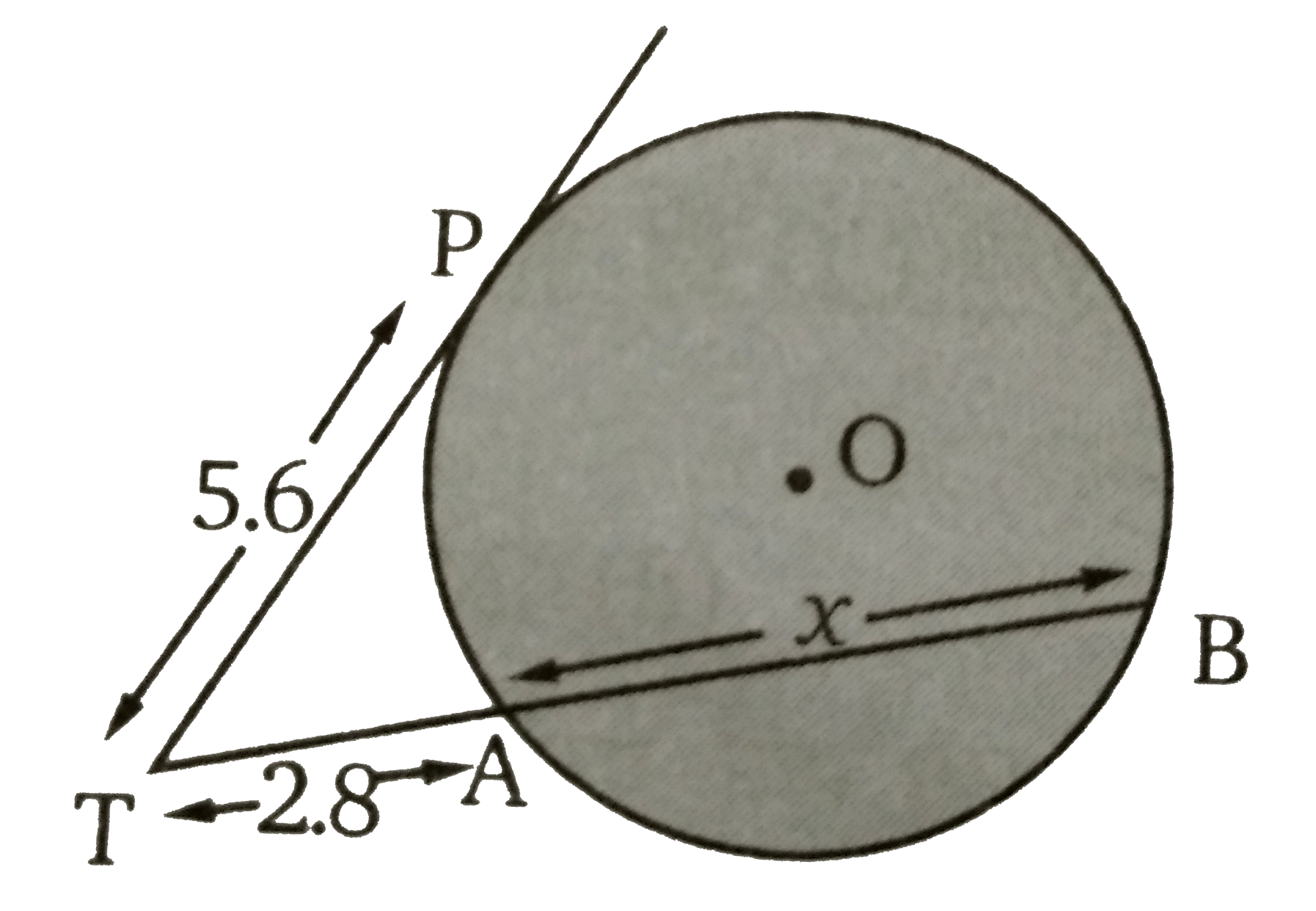
View Solutionदो पासो कि एक युगपत फेक में P (A या B ) का मान ज्ञात कीजिए। यदि A का अर्थ है "पासो पर योगफल 11 प्राप्त करना" तथा B का अर्थ है " प्रत्येक पासे पर एक सम संख्या, एक विषम संख्या है।"
View Solutionसमुच्चय {x:x एक अभाज्य संख्या, जो कि संख्या 30 की भाजक है } को रोस्टर रूप में लिखिय।
View Solutionसम्बन्ध R={(x,x3):x,10से कम एक अभाज्य संख्या है} को रोस्टर रूप में लिखिए ।
View Solutionनिम्न कथन पर विचार कीजिये ''P(n)=n2−n+41 एक अभाज्य संख्या है'' तो इनमे से कौन-सा एक सत्य है?
View Solutionयदि z−αz+α(α∈R) एक शुद्ध रूप से काल्पनिक संख्या है तथा |z|=2 है तो α का एक मान है
View Solutionयदि z एक सम्मिश्र संख्या है, तो निम्न में से कौन-सा कथन सत्य है?
View Solutionसिद्ध कीजिये कि3−2√5 एक अपरिमेय संख्या है।
View Solutionयदि x एक वास्तविक संख्या है तो |x|<4 का हल होगा-
View Solutionनिम्नलिखित कथनो में सत्य एवं असत्य कथन की पहचान करे (2sqrt5)/(3sqrt15) एक अपरिमेय संख्या है
View Solutionदो परिमेय संख्याओं का गुणनफल −2827 है। यदि उनमे से एक संख्या 49 है तो दूसरी संख्या क्या है ?
View Solutionयदि संख्या 354Y2, 6 का एक गुणज है तो Yअंक का मान क्या हो सकता है?
View Solutionएक समबहुभुज की भुजाओं की संख्या ज्ञात कीजिए यदि उसका प्रत्येक बहिष्कोण 20∘ हो।
View Solution
