सिद्ध कीजिये की किसी त्रिभुज का केन्द्रक तथा उसकी भुजाओं के मध्य बिन्दुओ को मिलाने वाले त्रिभुज का केन्द्रक समान होता है|
माना ABC एक त्रिभुज है| तब केन्द्रक के निर्देशांक
G1(x1+x2+x33,y1+y2+y33)
माना D,E व F क्रमशः BC,CA व AB के निर्देशांक है| तब
D≡D(x2+x32,y2+y32)
E=E(x1+x32,y1+y32)
तथा f≡F(x1+x22,y1+y22),
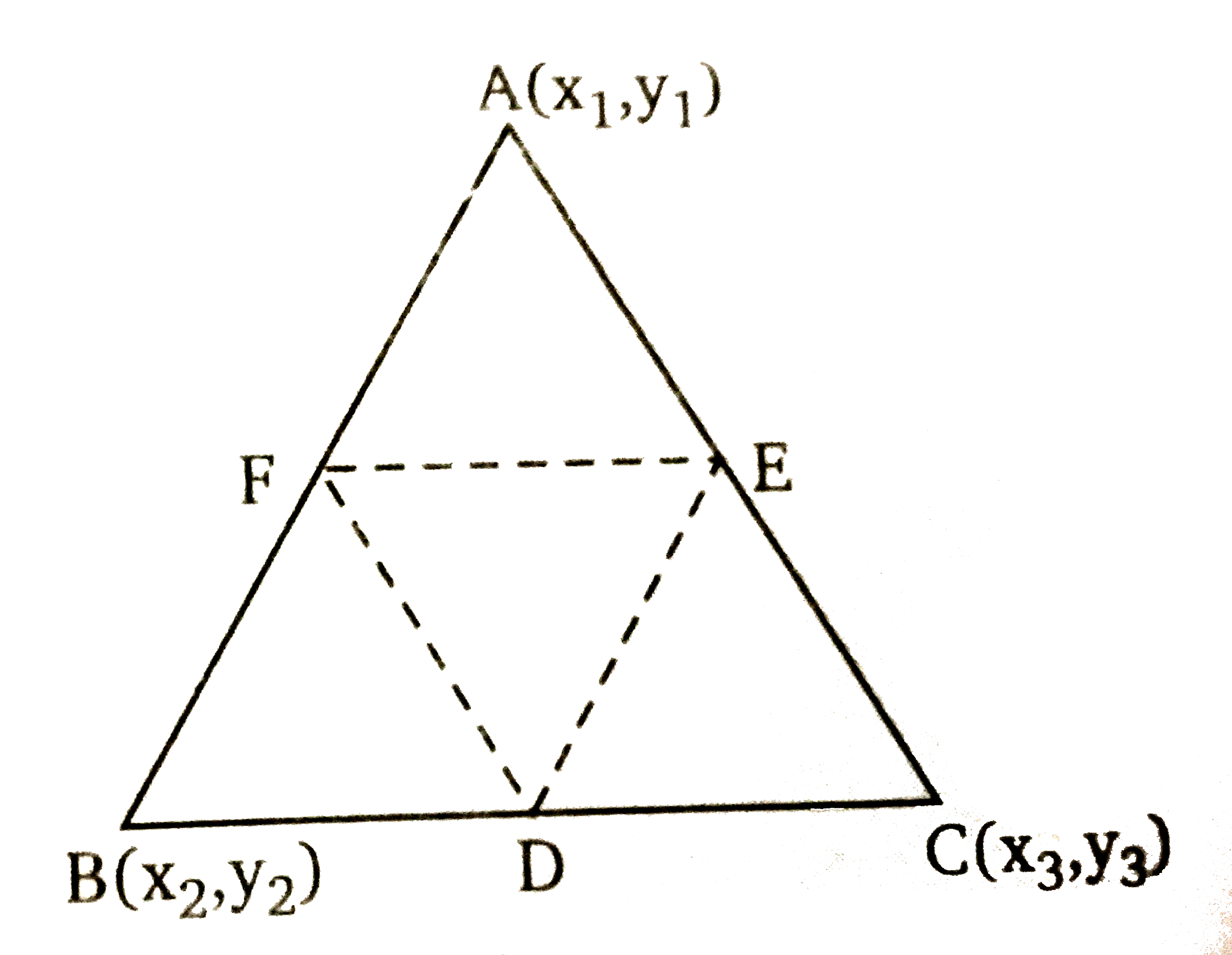
अब ΔDEF के केन्द्रक G2 का निर्देशांक
=[13(x3+x22+x3+x12+x1+x22),13(y3+y22+y3+y12+y1+y22]
=(x1+x2+x33,y1+y2+y33)
स्पष्ट है की G1 व G2 एक ही बिंदु को प्रदर्शित करते है|
Topper's Solved these Questions
- निर्देशांक ज्यामिति BOOK - BALAJI PUBLICATIONCHAPTER - निर्देशांक ज्यामिति EXERCISE - अभ्यास प्रश्न 6.1
6 Videos
- निर्देशांक ज्यामिति BOOK - BALAJI PUBLICATIONCHAPTER - निर्देशांक ज्यामिति EXERCISE - अभ्यास प्रश्न 6.2 (अतिलघु उत्तरीय प्रश्न)
11 Videos
- द्विघात समीकरण BOOK - BALAJI PUBLICATIONCHAPTER - द्विघात समीकरण EXERCISE - स्वमूल्यांकन परिक्षण
31 Videos
- पृष्ठीय क्षेत्रफल और आयतन BOOK - BALAJI PUBLICATIONCHAPTER - पृष्ठीय क्षेत्रफल और आयतन EXERCISE - स्वमूल्यांकन परीक्षण
23 Videos
Similar Questions
वह चतुर्थांश ज्ञात कीजिये जिसमें निम्न बिंदु स्थित है|
(i)(−1,−4) (ii)(4,1) (iii)(3,−2) (iv)(−3,1) (v)(7,2) (vi)(−3,−2) (vii)(−6,4) (viii)(2,−2)
View Solutionकिसी बिंदु का भुज किस चतुर्थांश में ऋणात्मक होता है?
View Solutionद्विघात समीकरण √3x2+10x−8√3=0 को हल कीजिए।
View Solution11 सेमी × 10 सेमी × 7 सेमी विमाओं वाला घनाभ बनाने के लिए 1.75 सेमी व्यास तथा 2 मिमी की मोटाई के कितने सिक्के पिघलाने पड़ेगें ?
View Solutionयदि मूलबिंदु O के सापेक्ष त्रिभुज ABC के शीर्षों के स्थिति सदिश क्रमशः (1,−1,2),(2,1,3) और (−1,2,−1) है| तथा इसके केन्द्रक का स्थिति सदिश ज्ञात कीजिए|
View Solutionपरवलय y2=4ax की नाभि तथा उस पर स्थित चर को मिलाने वाले रेखाखण्ड के मध्य - बिंदु का पथ एक परवलय है जिसकी नियता है :
View Solutionकिसी समबाहु त्रिभुज के आधार का समीकरण x+y=2 है तथा सामने के शीर्ष के निर्देशांक (2,1) है , त्रिभुज की शेष भुजाओ के समीकरण ज्ञात कीजिए ।
View Solutionकिसी त्रिभुज कि भुजाओ के मध्य बिन्दुओ के निर्देशांक क्रमशः (2,1),(−5,7) तथा (−5,5) है त्रिभुज कि भुजाओ के समीकरण ज्ञात कीजिए ।
View Solutionमाना A(2,−3) तथा B(−2,1) एक त्रिभुज ABC के शीर्ष है । यदि इस त्रिभुज का केन्द्रक सरल रेखा 2x+3y=1पर भ्रमण करता है तो शीर्ष C का बिन्दुपथ है -
View Solutionत्रिभुज का गुरुत्व केंद्र होता है।
View Solutionवह त्रिभुज जिसका लांबकेंद्र त्रिभुज का शीर्ष बिंदु होता है ,कहलाता है -
View Solution10सेमी त्रिज्या वाले वृत्त की त्रिज्याओं के मध्य बिन्दुओ का बिन्दुपथ होगा।
View Solutionकिसी त्रिभुज के शीर्षो से समान दूरी पर स्तिथ बिंदु का नाम लिखि।
View Solutionयदि किसी त्रिभुज के शीर्षो के स्थिति सदिश क्रमश: →a,→b,→c हो तो इस त्रिभुज के केन्द्रक का स्थिति सदिश होगा -
View Solutionकिसी त्रिभुज के शीर्ष बिन्दुओं के निर्देशांक (0,1),(2,0) और (-1,-2) है। उसकी भुजाओं के समीकरण ज्ञात कीजिए।
View Solutionमान A(2,−3) तथा B(−2,1) एक त्रिभुज ABC के शीर्ष है। यदि इस त्रिभुज का केन्द्रक सरल रेखा 2x+3y=1 पर भ्रमण करता है, तो शीर्ष C का बिन्दुपथ है:
View Solution
