सिद्ध कीजिये की बिंदु (x1,y1),(x2,y2) तथा (x3,y3) शीर्ष वाले त्रिभुज के केन्द्रक के निर्देशांक (x1+x2+x33,y1+y2+y33) है| यह भी सिद्ध कीजिये की मध्यमिकाएँ संगामि है|
माना A(x1,y1),B(x2,y2) तथा C(x3,y3) शीर्ष वाले ΔABC की मध्यकायें क्रमशः AD ,BE व CF है | इसलिए BC ,CA व AB के मध्य बिंदु क्रमशः D,E व F है|
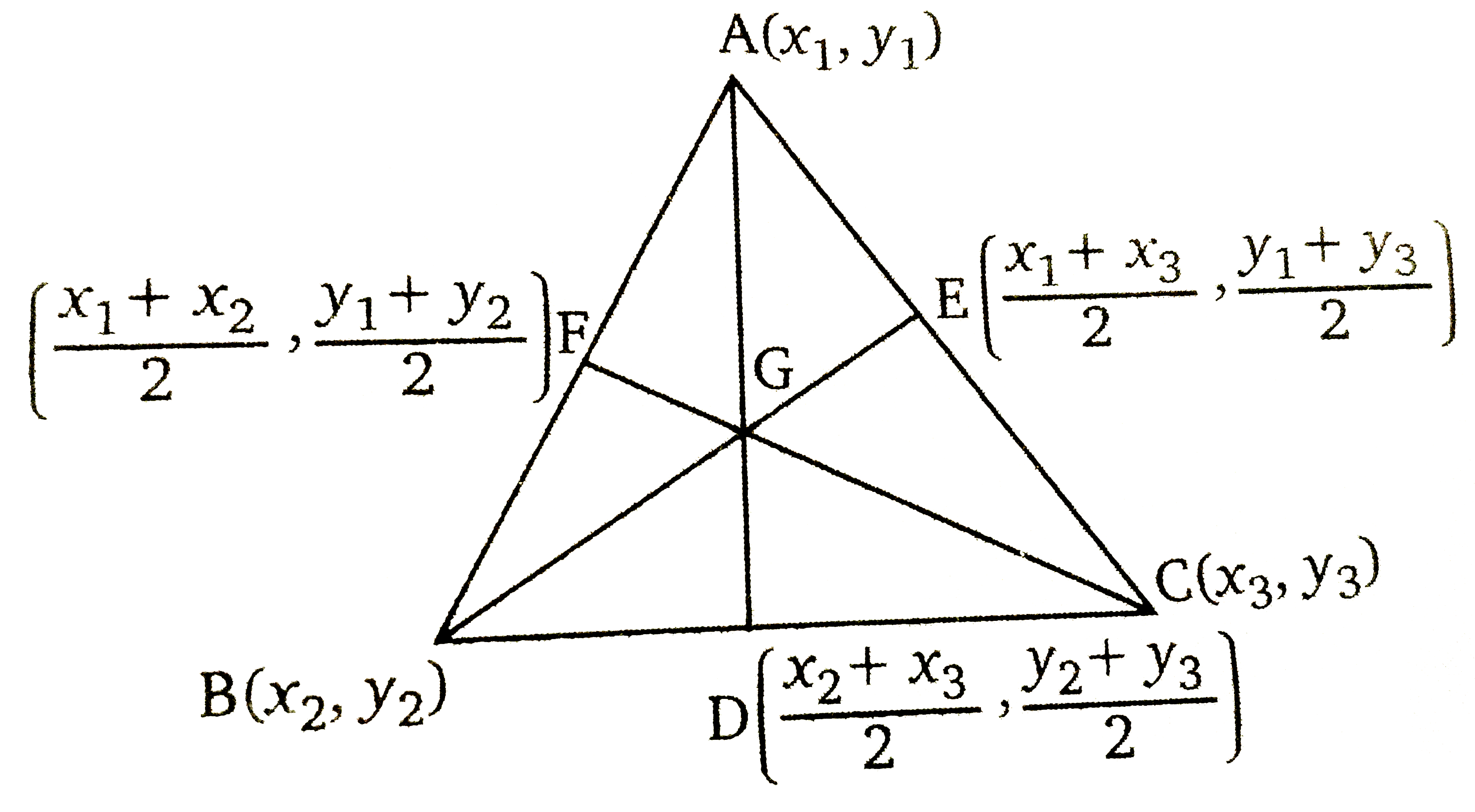
∵D के निर्देशांक (x2+x32,y2+y32) है तथा G के निर्देशांक AD को 2:1 के अनुपात में विभाजित करते है|
⎡⎢
⎢⎣1⋅x1(x2+x32)1+2,⋅1⋅y1+2(y2+y32)1+2⎤⎥
⎥⎦=(x1+x2+x33,y1+y2+y33)
अब E के निर्देशांक (x1+x32,y1+y22)
तथा G के निर्देशांक, DE को 2:1 के अनुपात में विभाजित करते है|
⎛⎜⎝1⋅x1+2(x1+x3)21+2,1⋅y2+2(y1+y2)21+2⎞⎟⎠=(x1+x2+x33,y1+y2+y33)
इसी प्रकार G के निर्देशांक CF को 2:1 के अनुपात में विभाजित करते है|
(x1+x2+x33,y1+y2+y_33)
इसलिए निर्देशांक (x1+x2+x33,y1+y2+y33) निर्देशांक वाला बिंदु G AD,BE व CF में उभयनिष्ट है तथा 2:1 के अनुपात में विभाजित करती है|अतः केन्द्रक के निर्देशांक
(x1+x2+x33,y1+y2+y33) है तथा मध्यकायें संगामी है|
Topper's Solved these Questions
- निर्देशांक ज्यामिति BOOK - BALAJI PUBLICATIONCHAPTER - निर्देशांक ज्यामिति EXERCISE - अभ्यास प्रश्न 6.1
6 Videos
- निर्देशांक ज्यामिति BOOK - BALAJI PUBLICATIONCHAPTER - निर्देशांक ज्यामिति EXERCISE - अभ्यास प्रश्न 6.2 (अतिलघु उत्तरीय प्रश्न)
11 Videos
- द्विघात समीकरण BOOK - BALAJI PUBLICATIONCHAPTER - द्विघात समीकरण EXERCISE - स्वमूल्यांकन परिक्षण
31 Videos
- पृष्ठीय क्षेत्रफल और आयतन BOOK - BALAJI PUBLICATIONCHAPTER - पृष्ठीय क्षेत्रफल और आयतन EXERCISE - स्वमूल्यांकन परीक्षण
23 Videos
Similar Questions
वह चतुर्थांश ज्ञात कीजिये जिसमें निम्न बिंदु स्थित है|
(i)(−1,−4) (ii)(4,1) (iii)(3,−2) (iv)(−3,1) (v)(7,2) (vi)(−3,−2) (vii)(−6,4) (viii)(2,−2)
View Solutionकिसी बिंदु का भुज किस चतुर्थांश में ऋणात्मक होता है?
View Solutionद्विघात समीकरण √3x2+10x−8√3=0 को हल कीजिए।
View Solution11 सेमी × 10 सेमी × 7 सेमी विमाओं वाला घनाभ बनाने के लिए 1.75 सेमी व्यास तथा 2 मिमी की मोटाई के कितने सिक्के पिघलाने पड़ेगें ?
View SolutionTheorem : The area of a triangle the coordinates of whose vertices are (x1;y1);(x2;y2)and(x3;y3) is 1/2|(x_1(y_2-y_3)+x_2(y_3-y_1)+x_3(y_1-y_2)|
View SolutionIf the points (x1,y1),(x2,y2)and(x3,y3) be collinear, show that: y2−y3x2x3+y3−y1x3x2+y1−y2x1x2=0
View Solutionयदि तीन बिंदु (x1,y1),(x2,y2) तथा (x3,y3) संरेख है तो सिद्ध कीजिए की
(x3−x1)(y2−y1)=(x2−x1)(y3−y1)
View SolutionIf (x1,y1),(x2,y2) and (x3,y3) are the feet of the three normals drawn from a point to the parabola y2=4ax, then x1−x2y3+x2−x3y1+x3−x1y2 is equal to
View Solutionx1,x2,x3 மற்றும் y1,y2,y3 ஆகியவை ஒரே பொது விகிதம் கொண்ட பெருக்குத் தொடர்முறையில் இருந்தால், (x1,y1),(x2,y2),(x3,y3) என்ற புள்ளிகள்
View Solutionयदि x1,x2,x3 और y1,y2,y3 गुणोत्तर श्रेढ़ी में हैं, तथा दोनों का सार्वानुपात (common ratio) समान है, तब बिन्दु (x1,y1),(x2,y2) और (x3,y3)
View SolutionA triangle has vertices Ai(xi,yi)fori=1,2,3 If the orthocentre of triangle is (0,0), then prove that
∣x2−x3y2−y3y1(y2−y3)+x1(x2−x3)
x3−x1y2−y3y2(y3−y1)+x1(x3−x1)
x1−x2y2−y3y3(y1−y2)+x1(x1−x2)∣=0
View SolutionIf the points (x1,y1),(x2,y2), and (x3,y3) are collinear show that y2−y3x2x3+y3−y1x3x1+y1−y2x1x2=0
View SolutionIf the join of (x1,y1) and (x2,y2) makes on obtuse angle at (x3,y3), then prove that (x3−x1)(x3−x2)+(y3−y1)(y3−y2)<0
View SolutionProve that the points : (x1,y1),(x2,y2),(x3,y3)
are collinear if ⎡⎢⎣x1y11x2y21x3y31⎤⎥⎦=0
View SolutionIf x1,x2,x3 and y1,y2,y3 are both in G.P. with the same common ratio, then the points (x1,y1),(x2,y2) and (x3,y3)
View SolutionIf (x1,y1),(x2,y2) and (x3,y3) are the feet of the three normals drawn from a point to the parabola y2=4ax, then x1−x2y3+x2−x3y1+x3−x1y2 is equal to
View Solution
