एक त्रिभुज ABC का ∠B तथा ∠C का अर्द्धक विपरीत भुजा पर क्रमशः D तथा E में मिलता है । यदि DE।।BC तो सिद्ध कीजिए कि त्रिभुज समिद्विबाहु है ।
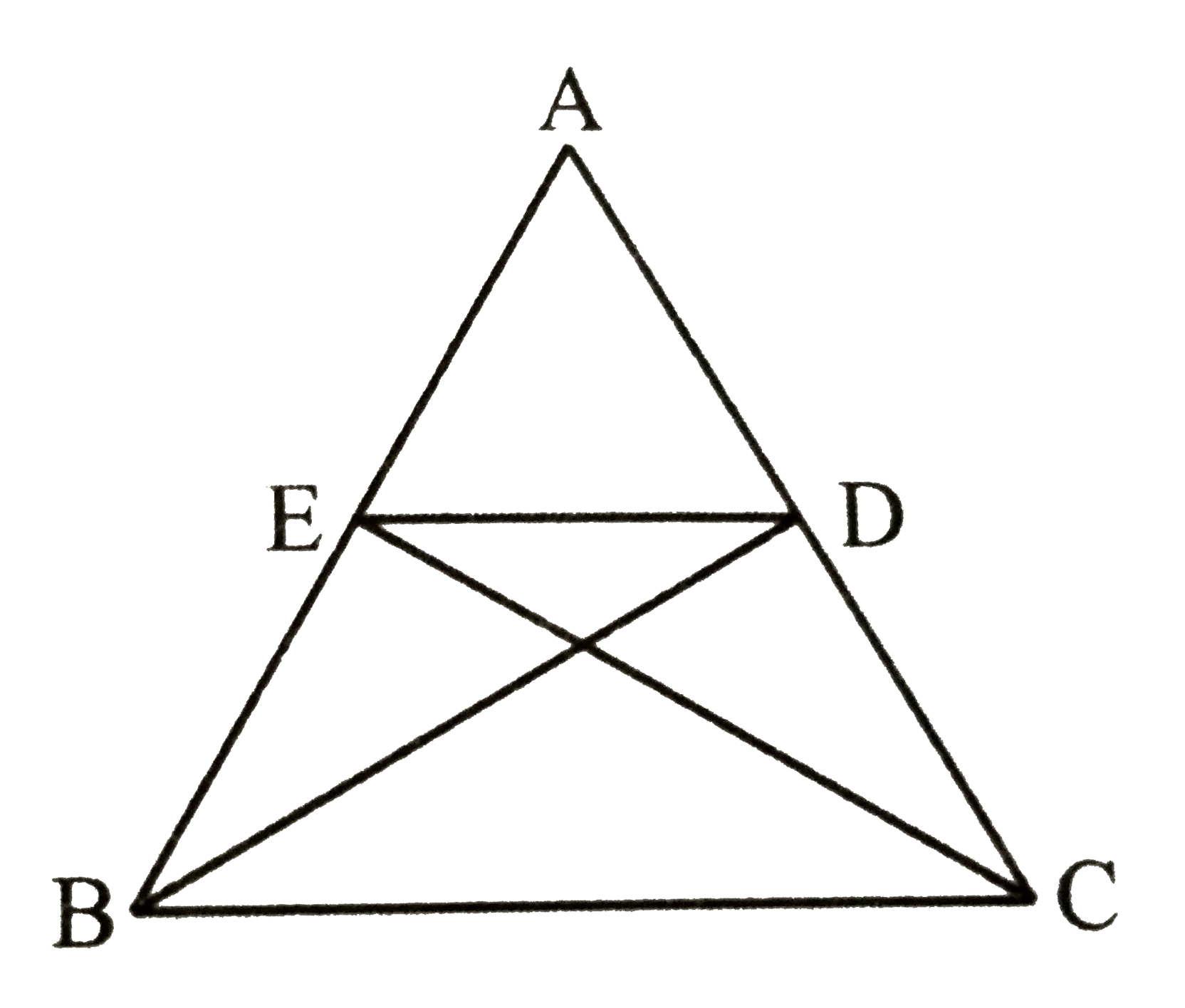
यहाँ △ABC है जिसमे ∠B तथा ∠C का अर्द्धक भुजा एक तथा AB पर क्रमशः बिन्दु D तथा E पर मिलता है ।
हमे सिद्ध करना है कि AB = AC
अब △ABC में, ∠B का अर्द्धक BD है । इसलिए,
ABBC=ADDC ...(1)
△ABC में CE,∠C का अर्द्धक है इसलिए,
ACBC=AEBE ...(2)
अब , DE।।BC तब आधारभूत समानुपातिक प्रमेय के विलोम द्वारा,
AEBE=ADDC ...(3)
समी० (1), (2) तथा (3) से, ABBC=ACBC⇒AB=AC
अतः △ABC समद्विबाहु है ।
Topper's Solved these Questions
- त्रिभुज BOOK - BALAJI PUBLICATIONCHAPTER - त्रिभुज EXERCISE - अभ्यास प्रश्न 7.1
9 Videos
- त्रिभुज BOOK - BALAJI PUBLICATIONCHAPTER - त्रिभुज EXERCISE - अभ्यास प्रश्न 7.2
17 Videos
- त्रिकोणमितीय अनुपात एव असमिकाएँ BOOK - BALAJI PUBLICATIONCHAPTER - त्रिकोणमितीय अनुपात एव असमिकाएँ EXERCISE - स्वमूल्यांकन परीक्षण
35 Videos
- दो चर वाले रैखिक समीकरण युग्म BOOK - BALAJI PUBLICATIONCHAPTER - दो चर वाले रैखिक समीकरण युग्म EXERCISE - स्वमूल्यांकन परीक्षण
29 Videos
Similar Questions
दी गई आकृति में DE∣∣BC यदि AD=2.5 सेमी, DB = 3 सेमी तथा AE = 3.75 सेमी है तो AC का मान ज्ञात कीजिए |
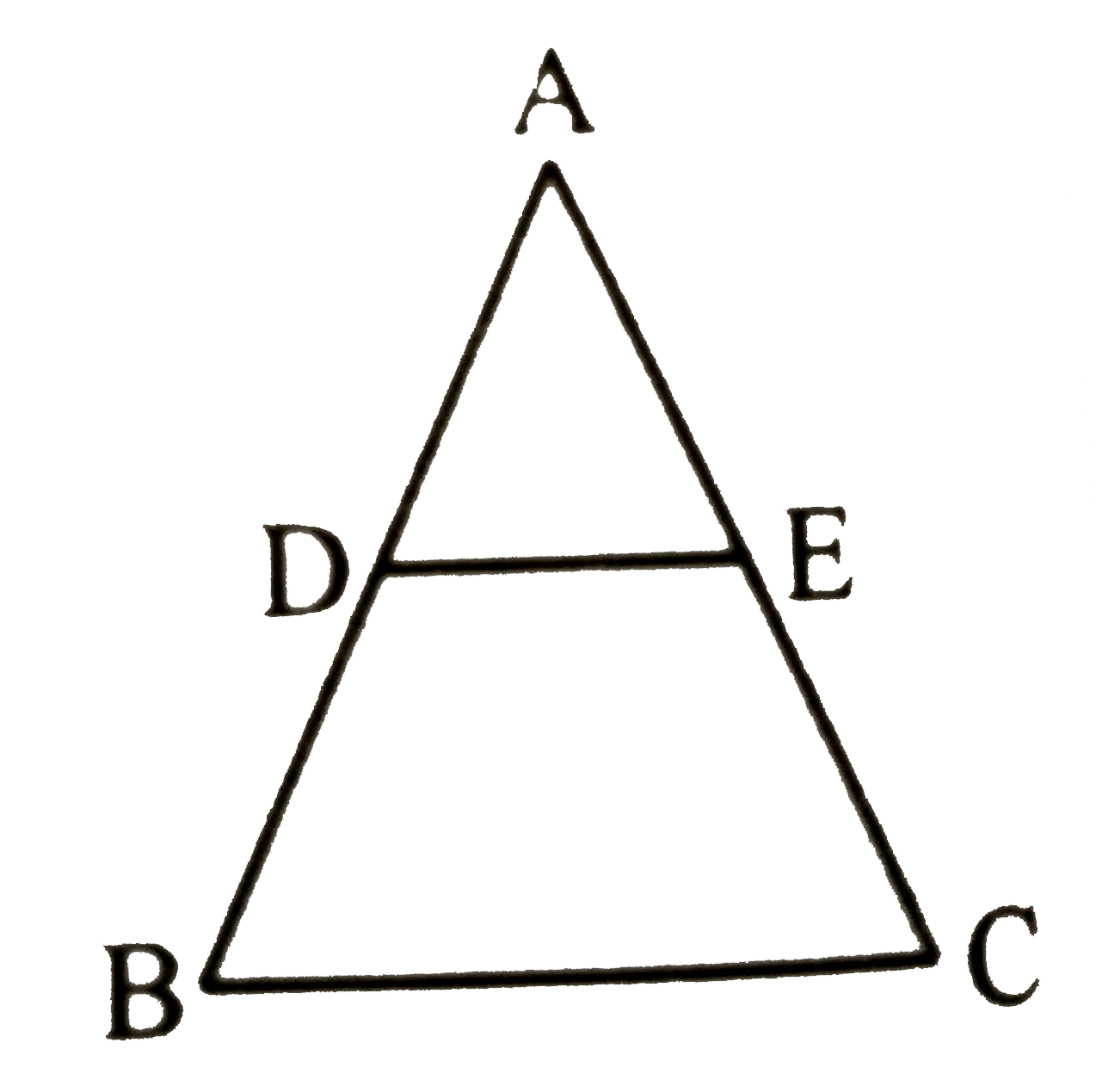
View Solutionदी गई आकृति में △ACB~△APQ है यदि BC=8 सेमी०, PQ=4 सेमी०, BA = 6.5 सेमी०, AP = 2.8 सेमी० है तो CA तथा AQ ज्ञात कीजिए |

View Solutionयदि cosθ=1√122, तब sinθ व tanθ के मान ज्ञात कीजिए.
View Solutionकिसी भिन्न के अंश से यदि 1 घटाया जाये तो वह 13 तथा यदि हर में 8 जोड़ा जाये तो वह 14 हो जाती है। भिन्न ज्ञात कीजिए।
View SolutionDetermine the point of symmetry of a regular hexagon.
View SolutionMatch the following Column A to Column B

View SolutionMatch the following Column A to Column B

View SolutionMatch the following Column A to Column B

View SolutionThe inequation represented by the graph given below is :
View SolutionThe inequation that best describes the graph given below is _________
View SolutionThe inequation that best describes the following graph is _________
View Solutionमाना A(2,−3) तथा B(−2,1) एक त्रिभुज ABC के शीर्ष है । यदि इस त्रिभुज का केन्द्रक सरल रेखा 2x+3y=1पर भ्रमण करता है तो शीर्ष C का बिन्दुपथ है -
View Solutionमान A(2,−3) तथा B(−2,1) एक त्रिभुज ABC के शीर्ष है। यदि इस त्रिभुज का केन्द्रक सरल रेखा 2x+3y=1 पर भ्रमण करता है, तो शीर्ष C का बिन्दुपथ है:
View Solutionएक समतल निर्देशांकों अक्षों को A,B,C पर इस प्रकार मिलता है कि त्रिभुज ABC का केंद्रक (1,2,3) है तो समतल का समीकरण होगा
View Solutionएक त्रिभुज का एक शीर्ष (1,2) पर है तथा इससे होकर जाने वाली दो भुजाओं के मध्य - बिन्दु (−1,1) और (2,3) हैं , तो इस त्रिभुज का केन्द्रक है
View SolutionIn the given fig. If DE||BC Find EC.
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/MATH_241_X_SQP_E01_021_Q01.png" width="80%"gt
View Solution
