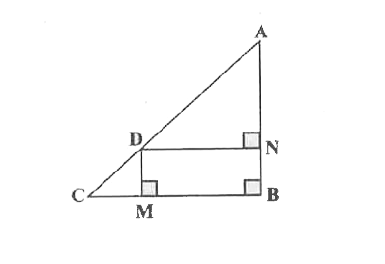
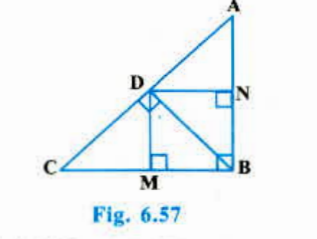
दी गई आकृति में, एक समकोण त्रिभुज ABC है जो B पर समकोण है | तथा B से AC पर एक लम्ब है जिसका निचला भाग D है यदि DM⊥BC तथा DN⊥AB है तो सिद्ध कीजिए कि
(i)(DM)2=DN×MC
(ii) (DN)2=DM×AN
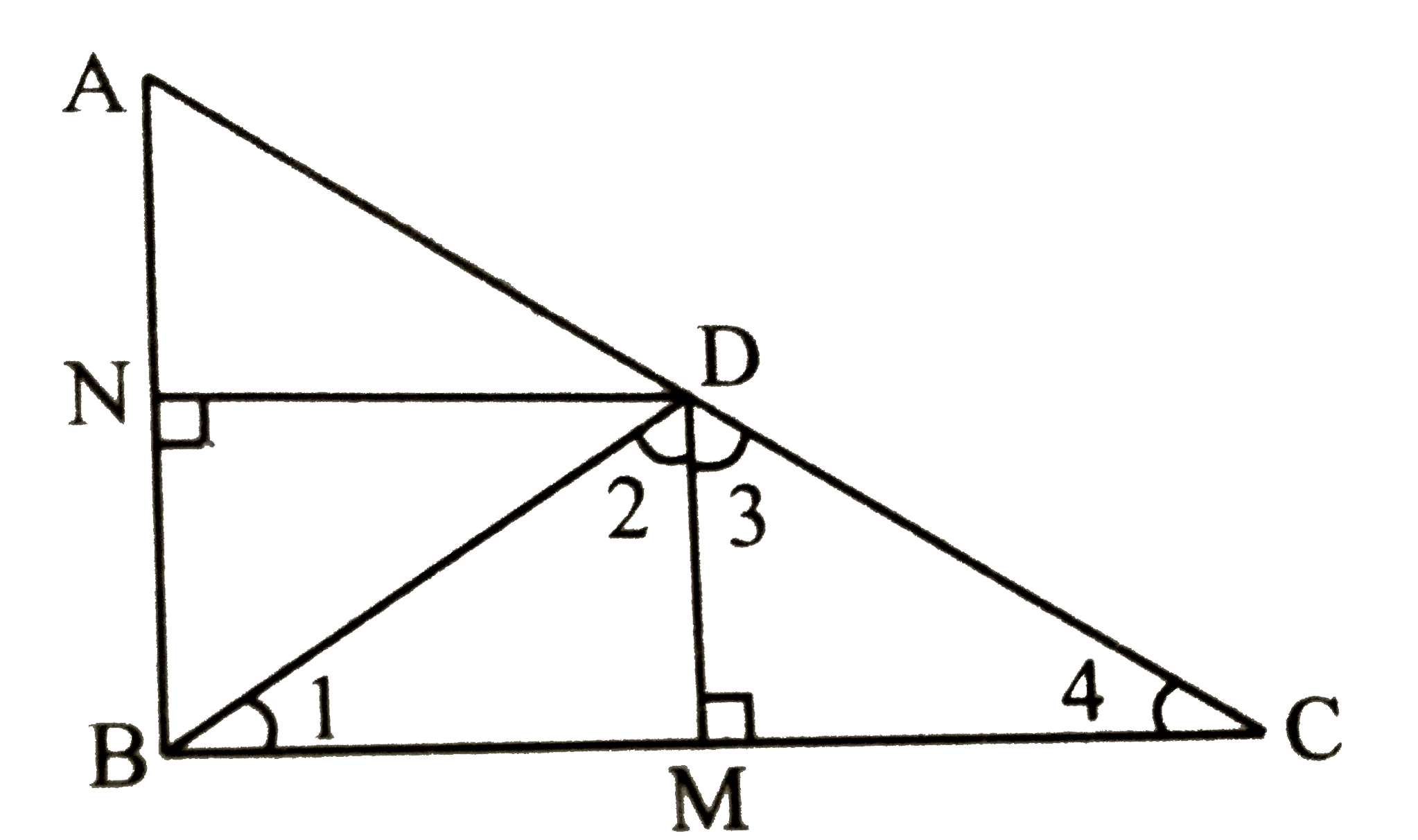
यहाँ स्पष्ट है कि
AB,BC पर लम्ब है तथा DN, AB पर लम्ब है |
⇒AB⊥BC तथा DN⊥AB
⇒CB∣∣DN
⇒BMDN एक आयत है |
इसलिए, BM=ND
अब △BMD में,
∠1+∠BMD+∠2=180∘
⇒∠1+90∘+∠2=180∘⇒∠1+∠2=90∘
इस तरह △DMC में, ∠3+∠4=90∘
तथा चूँकि BD⊥AC∠2+∠3=90∘
अतः ∠1+∠2=90∘=∠2+∠3
⇒∠1=∠3
तथा ∠3+∠4=90∘=∠2+∠3
अतः समरूपता की AA-कसौटी द्वारा,
△BMD~△DMC
⇒⋅BMDM=MDMC (आधारभूत समानुपातिक प्रमेय द्वारा )
⇒DNDM=DMMC
⇒(DM)2=DN×MC (∵ND=BM)
(ii) (1) की तरह ही हम प्राप्त कर सकते है |
△BND~△DNA
⇒BNDN=NDNA (आधारभूत समानुपातिक प्रमेय द्वारा)
⇒DMDN=DNAN
⇒(DN)2=DM×AN (∵BN=DN)
Topper's Solved these Questions
- त्रिभुज BOOK - BALAJI PUBLICATIONCHAPTER - त्रिभुज EXERCISE - अभ्यास प्रश्न 7.1
9 Videos
- त्रिभुज BOOK - BALAJI PUBLICATIONCHAPTER - त्रिभुज EXERCISE - अभ्यास प्रश्न 7.2
17 Videos
- त्रिकोणमितीय अनुपात एव असमिकाएँ BOOK - BALAJI PUBLICATIONCHAPTER - त्रिकोणमितीय अनुपात एव असमिकाएँ EXERCISE - स्वमूल्यांकन परीक्षण
35 Videos
- दो चर वाले रैखिक समीकरण युग्म BOOK - BALAJI PUBLICATIONCHAPTER - दो चर वाले रैखिक समीकरण युग्म EXERCISE - स्वमूल्यांकन परीक्षण
29 Videos
Similar Questions
दी गई आकृति में DE∣∣BC यदि AD=2.5 सेमी, DB = 3 सेमी तथा AE = 3.75 सेमी है तो AC का मान ज्ञात कीजिए |
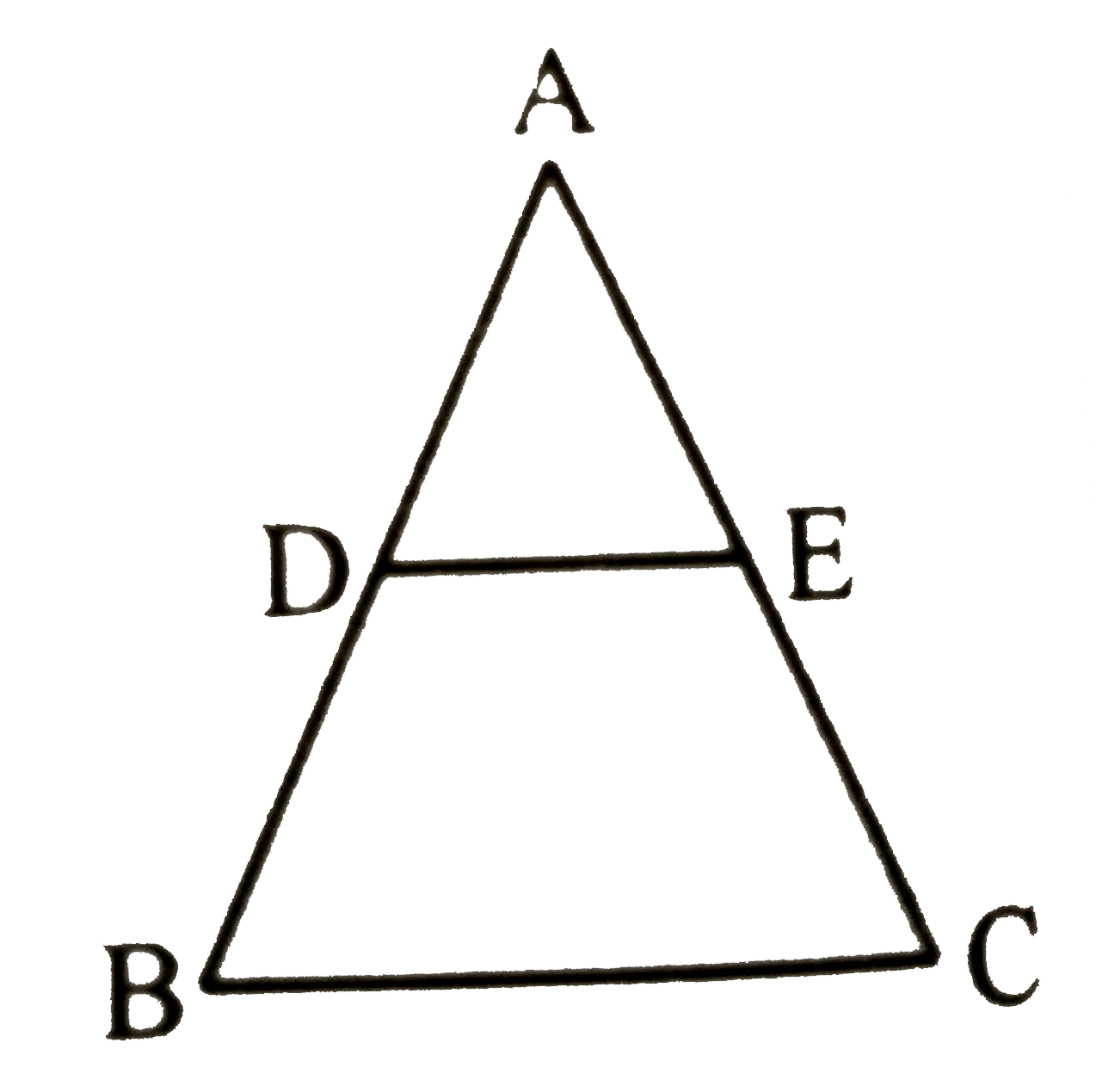
View Solutionदी गई आकृति में △ACB~△APQ है यदि BC=8 सेमी०, PQ=4 सेमी०, BA = 6.5 सेमी०, AP = 2.8 सेमी० है तो CA तथा AQ ज्ञात कीजिए |

View Solutionयदि cosθ=1√122, तब sinθ व tanθ के मान ज्ञात कीजिए.
View Solutionकिसी भिन्न के अंश से यदि 1 घटाया जाये तो वह 13 तथा यदि हर में 8 जोड़ा जाये तो वह 14 हो जाती है। भिन्न ज्ञात कीजिए।
View SolutionFig.4.134,ABC is a right triangle right angled at B and D is the foot of the wedicular dnem from Ben AC. If DM perp BC and DN perp AB, prove that ( i )DM^(2)=DN xx MC( ii) DN^(2)=DM xx AN
View SolutionIn Fig. 4.121, ABC is a right triangle right angled at B and D is the foot of the the perpendicular drawn from B on AC . If DM⊥BC and DN⊥AB , prove that: (FIGURE) DM2=DN×MC (ii) DN2=DM×AN
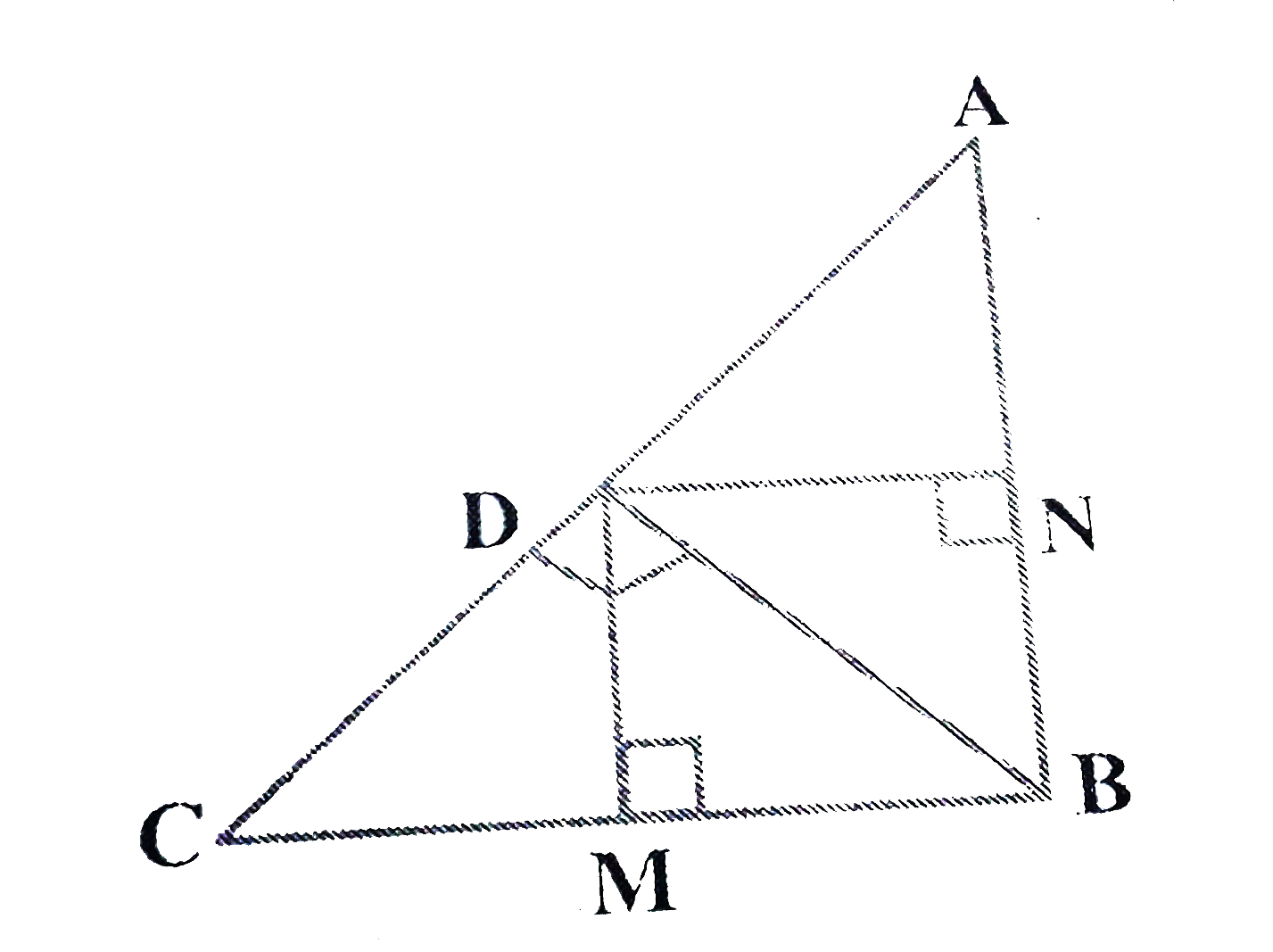
View Solutionआकृति 6.57 में D त्रिभुज ABC के कर्ण AC पर स्थित एक बिंदु है जबकि BD⊥AC तथा DM⊥BC और DN⊥AB है । सिद्ध कीजिए कि
(i) DM2=DN.MC (ii) DN2=DM.AN
View Solutionदी गई आकृति में बिंदु B ,C तथा D से गुजरने वाले वृत्त के बिंदु B तथा C पर AB तथा AC स्पर्श रेखाएं है। यदि ∠BAC=70∘ और ∠CBD=90∘ तो ∠BCD का मान है -
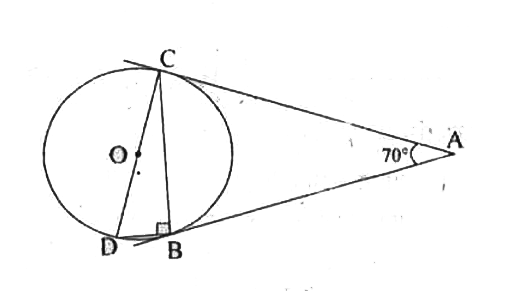
View SolutionIn Fig. D is point on hypotenuse AC of ΔABC,BD⊥ACDM⊥BCandDN⊥AB . Prove that :
(i) DM2=DN.MC , (ii) DN2=DM.AN
View Solutionमाना एक दीर्घवृत्त कि नाभियां S तथा S' है तथा इसके लघु अक्ष का कोई एक शीर्ष B है। यदि ΔS'BS एक समकोण त्रिभुज है जिसका समकोण B पर है तथा ΔS'BS का क्षेत्रफल 8 वर्ग इकाई है, तो दीर्घवृत्त की एक नाभिलम्ब जीवा की लम्बाई है
View SolutionIn Fig. D is point on hypotenuse AC of ΔABC,BD⊥ACDM⊥BCandDN⊥AB . Prove that :
(i) DM2=DN.MC , (ii) DN2=DM.AN

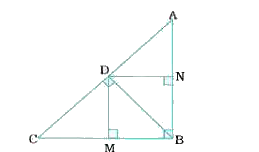
View SolutionIn the given figure, D is a point on hypotenuse AC of △ABC, such that BD⊥AC,DM⊥BC and DN⊥AB. Prove that :
DM2=DN⋅MC
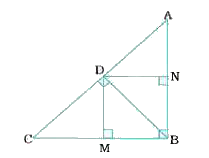
View SolutionIn the given figure, D is a point on hypotenuse AC of △ABC, such that BD⊥AC,DM⊥BC and DN⊥AB. Prove that :
DN2=DM⋅AN
View SolutionIn Fig, D is a point on hypotenuse AC of ΔABC, such that BD⊥AC, DM⊥BC and DN⊥AB.Prove that :- DM2=DN.MC
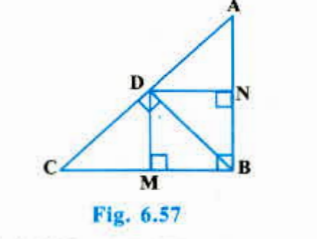
View SolutionIn Fig, D is a point on hypotenuse AC of ΔABC, such that BD⊥AC, DM⊥BC and DN⊥AB.Prove that :- DN2=DM.AN
View SolutionIn triangle ABC , AD bot BC and BE bot AC , AD and BE intersect each other at F. If BF = AC, then the measure of angle ABC is: त्रिभुज ABC में, AD bot BC है तथा BE bot AC है | AD और BD एक दूसरे को F पर काटते है | यदि BF = AC है, तो angle ABC का माप क्या होगा ?
View Solution
