दिये गये चित्र में, दो त्रिभुज ABC तथा DBC एक ही आधार पर स्थित है | यदि AD, BC, को O पर प्रतिच्छेद करती है तो दिखाइए कि,
(△ABC)का क्षेत्रफल(△BCD)का क्षेत्रफल=AODO
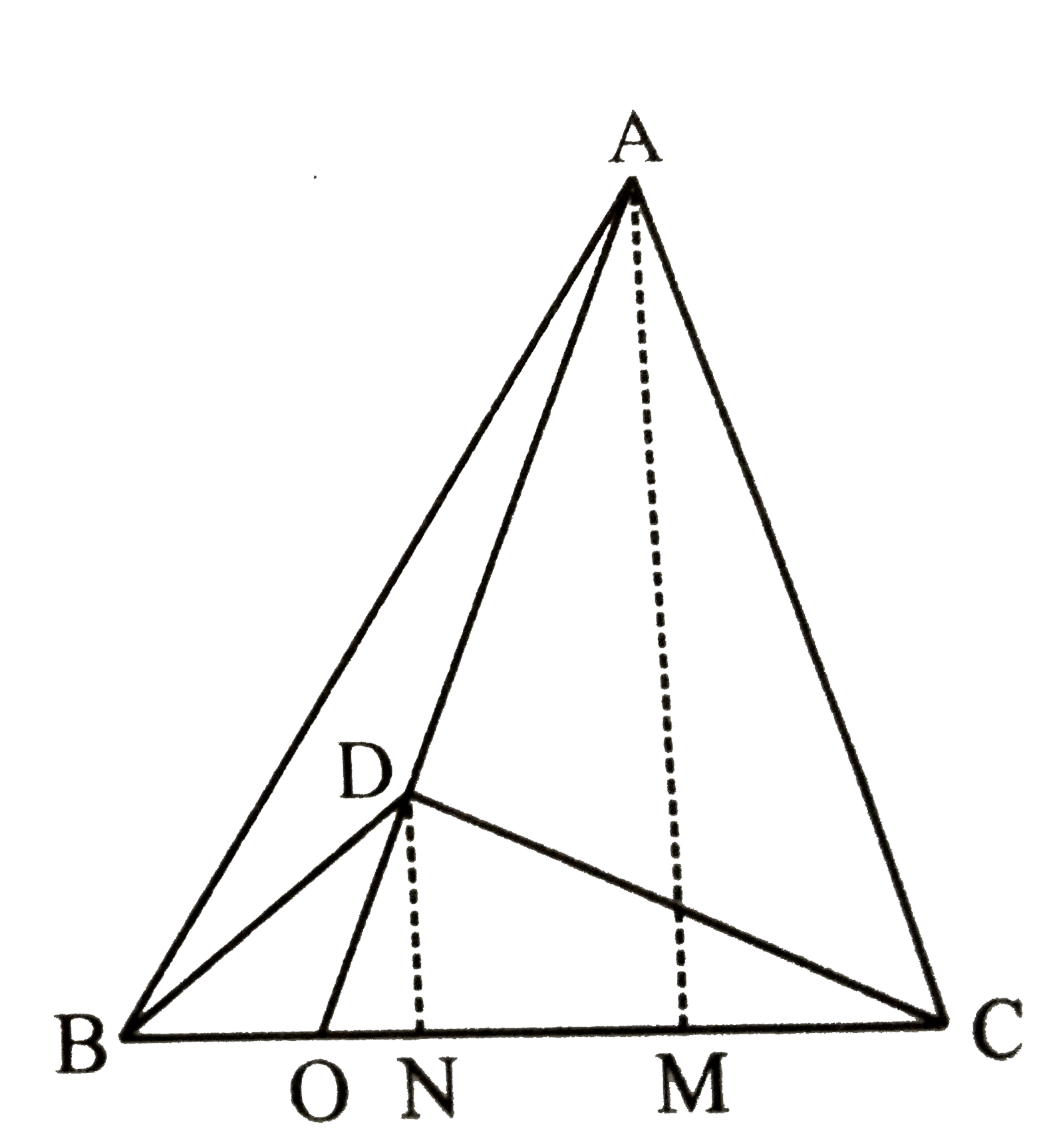
यहाँ दो त्रिभुज ABC तथा BCD एक ही आधार पर स्थित है तथा AD, BC को O पर प्रतिच्छेद करती है तब हमे सिद्ध करना है कि
(△ABC)का क्षेत्रफल(△BCD)का क्षेत्रफल=AODO
अब AM⊥BC तथा DN⊥BC खींचा
△AMO तथा △DNO, में, ∠M=∠N (प्रत्येक =90∘)
∠AOM=∠DON
तब समरूपता की AA-कसौटी द्वारा,
△AMO~△DNO
इसलिए आधारभूत समानुपातिक प्रमेय द्वारा, AODO=AMDN=12×BC×AM12×BC×DN (अंश तथा हर दोनों में 12BC से गुणा करने पर ),
=(△ABC)का क्षेत्रफल(△BCD)का क्षेत्रफल
Topper's Solved these Questions
- त्रिभुज BOOK - BALAJI PUBLICATIONCHAPTER - त्रिभुज EXERCISE - अभ्यास प्रश्न 7.1
9 Videos
- त्रिभुज BOOK - BALAJI PUBLICATIONCHAPTER - त्रिभुज EXERCISE - अभ्यास प्रश्न 7.2
17 Videos
- त्रिकोणमितीय अनुपात एव असमिकाएँ BOOK - BALAJI PUBLICATIONCHAPTER - त्रिकोणमितीय अनुपात एव असमिकाएँ EXERCISE - स्वमूल्यांकन परीक्षण
35 Videos
- दो चर वाले रैखिक समीकरण युग्म BOOK - BALAJI PUBLICATIONCHAPTER - दो चर वाले रैखिक समीकरण युग्म EXERCISE - स्वमूल्यांकन परीक्षण
29 Videos
Similar Questions
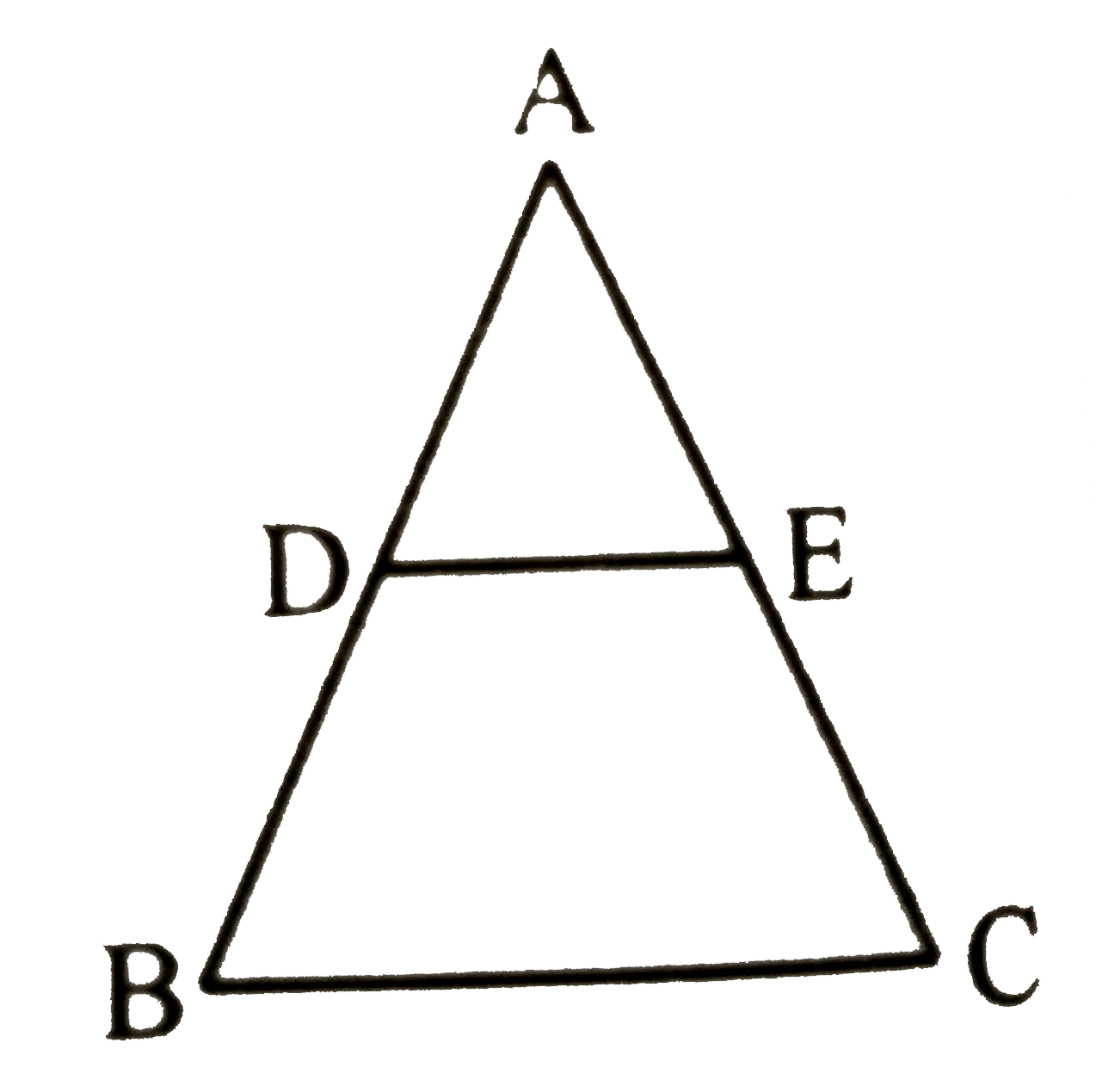
दी गई आकृति में DE∣∣BC यदि AD=2.5 सेमी, DB = 3 सेमी तथा AE = 3.75 सेमी है तो AC का मान ज्ञात कीजिए |
View Solutionदी गई आकृति में △ACB~△APQ है यदि BC=8 सेमी०, PQ=4 सेमी०, BA = 6.5 सेमी०, AP = 2.8 सेमी० है तो CA तथा AQ ज्ञात कीजिए |

View Solutionयदि cosθ=1√122, तब sinθ व tanθ के मान ज्ञात कीजिए.
View Solutionकिसी भिन्न के अंश से यदि 1 घटाया जाये तो वह 13 तथा यदि हर में 8 जोड़ा जाये तो वह 14 हो जाती है। भिन्न ज्ञात कीजिए।
View SolutionMatch the following Column A to Column B

View Solutionएक ΔABC में, AB = ri + j, AC =si-j, यदि त्रिभुज का क्षेत्रफल इकाई परिमाण का है। तब,
View SolutionIn triangle ABC AD, BE, CF are medians. If the area of the triangle DGC is 20cm^2 , then the area of triangle AGF + the area of triangle BGF is equal to: त्रिभुज ABC में, AD, BE और CF मध्यरेखा हैं और G त्रिभुज का केन्द्रक है। यदि त्रिभुज DGC का क्षेत्रफल 20cm^2 है, तो त्रिभुज AGF का क्षेत्रफल+ त्रिभुज BGF का क्षेत्रफल किसके बराबर है:
View SolutionIn an isosceles triangle ABC with AB = AC and AD is perpendicular to BC, if AD = 6 cm and the perimeter of triangle ABC is 36 cm, then the area of triangle ABC is: एक समद्विबाह त्रिभुज ABC में AB=AC और AD, BC पर लंबवत है, यदि AD = 6 सेमी और ABC की परिधि 36 सेमी है, तो ABC का क्षेत्रफल है
View SolutionIn an isosceles triangle ABC, AB=AC and AD is perpendicular to BC at D. If AD = 8 cm and perimeter of triangle ABC is 64cm, then the area of triangle ABC एक समद्विबाहु त्रिभुज ABC में, AB= AC और AD, BC पर लंबवत है। यदि AD =8 सेमी और ABC की परिधि 64 cm है, तो ABC का क्षेत्रफल है:
View SolutionIn triangle ABC , F and E are the points on sides AB and AC respectively, such that FE || BC and FE divides the triangle in two parts of equal area. If AD bot BC and AD intersect FE at G, then GD: AG = ? triangle ABC में F और E क्रमशः भुजा AB और AC पर स्थित ऐसे बिंदु हैं कि FE || BC है तथा FE त्रिभुज को बराबर क्षेत्रफल वाले दो भागों में विभाजित करती है | यदि AD bot BC है और AD, FE को G पर काटती है, तो GD: AG = ?
View SolutionA circle is inscribed in triangle ABC , touching AB at P, BC at Q and AC at R. If AR=5 cm, RC= 6 cm and AB=12 cm, then perimeter of triangle ABC is: एक वृत्त किसी त्रिभुज ABC में समाहित है जो AB को P पर, BC को Q पर तथा AC को R पर स्पर्श करता है | यदि AR =5 सेमी और AB = 12 सेमी है, तो त्रिभुज ABC का परिमाप ज्ञात करें |
View SolutionThe area of a triangle ABC is one unit. DE is a straight line parallel to BC , joining the points D and E on AB and AC respectively such that AD : DB = 1 : 6. The ratio of the areas of the triangles ADE and ABC is : एक त्रिभुज ABC का क्षेत्रफल 1 इकाई है | DE, BC के समानांतर एक सीधी रेखा है जो क्रमशः AB और AC पर स्थित बिंदु D तथा E को इस प्रकार जोड़ती है कि AD : DB = 1 : 6 है | त्रिभुज ADE और ABC के क्षेत्रफल में अनुपात ज्ञात करें |
View SolutionIn triangle ABC , AD bisects angle A and intersects BC at D. If BC = a ,AC = b and AB = c, then BD = ? त्रिभुज ABC में, AD कोण A को समद्विभाजित करता है तथा BC को D पर काटता है | यदि BC = a, AC = b और AB = c है, तो BD = ?
View SolutionIn triangle ABC , D is a point on side AB, such that, BD = 2cm and DA = 3cm. E is a point on BC such that DE || AC and AC = 4 cm. Then (Area of triangle BDE ): (Area of trapezium ACED) is: त्रिभुज ABC में, D, भुजा AB पर स्थित ऐसा बिंदु है कि BD = 2 सेमी और DA =3 सेमी है | E, BC पर स्थित ऐसा बिंदु है कि DE || AC है और AC =4 सेमी है | तो त्रिभुज (BDE का क्षेत्रफल ) : (समलम्ब ACED का क्षेत्रफल) ज्ञात करें |
View SolutionIt is given that triangle ABC ~ triangle PRQ and that Area ABC : Area PRQ = 16: 169. If AB = x, AC = y, BC = z (all in cm), then PQ is equal to: यह दिया गया है कि triangle ABC ~ triangle PRQ है तथा ABC का क्षेत्रफल : PRQ का क्षेत्रफल =16 :169 @ | यदि AB =x, AC =y, BC =z ( सभी सेमी में ) है, तो PQ का मान क्या होगा ?
View Solution
