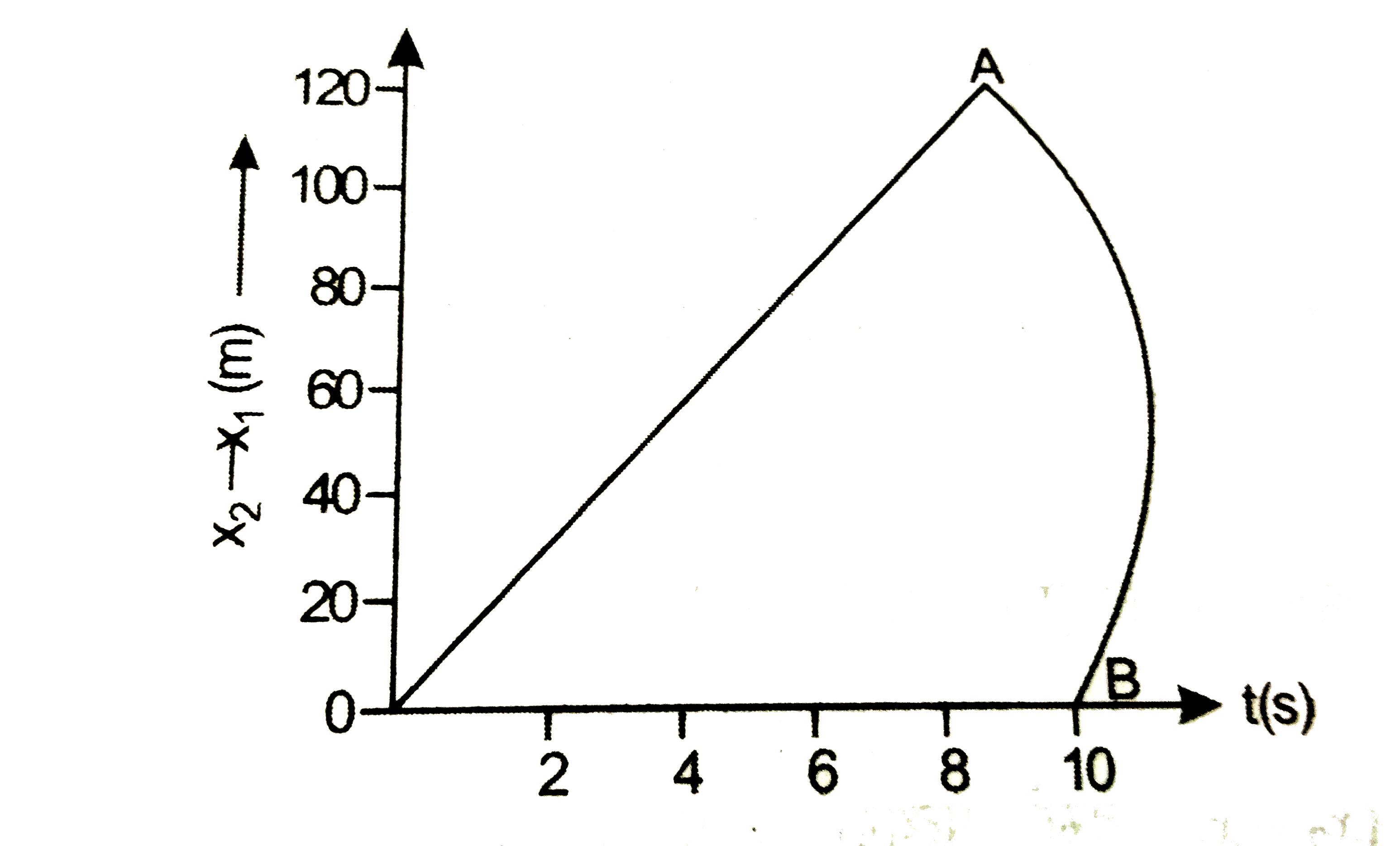
किसी 200 मीटर ऊंची खड़ी चट्टान के किनारे से दो पत्थरों को एक साथ ऊपर की ओर 15 मीटर/सेकण्ड तथा 30 मी0/से0 की प्रारम्भिक चाल से फेंका जाता है। इसका सत्यापन कीजिए कि नीचे दिखाया गया ग्राफ पहले पत्थर के सापेक्ष दूसरे पत्थर की आपेक्षिक स्थिति का समय के साथ परिवर्तन को प्रदर्शित करता है। वायु के प्रतिरोध को नगण्य मानिये और यह मानिये कि जमीन टकराने के बाद पत्थर ऊपर की ओर उछलते नहीं । मान लीजिए g=10m/s2. ग्राफ के रेखीय व वक्रीय भागों के लिए समीकरण लिखिए।
चट्टान के किनारे की ऊंचाई (x0)=200 मीटर
त्वरण (a)=−10मीटर/सेकण्ड2
पहले पत्थर के लिए
पत्थर का वेग u1=15 मीटर/सेकण्ड
समीकरण x1=x0+u1t+12at2
=200+15t+12(−10)t2
x1=20+15t−5t2 ………..i
जब पत्थर जमीन से टकराता है तब
x1=0
∴0=200+15t−5t2
अथवा t2−3t−40=0
अथवा t2−8t+5t−40=0
t(t−8)+5(t−8)=0
अथवा (t−8)(t+5)=0
अथवा t=8s
अथवा t=−5s
परंतु t=−5s सम्भव नहीं है।
जमीन से टकराने में लगा समय
∴t=8s
दूसरे पत्थर के लिए
पत्थर की चाल u2=30 मीटर/सेकण्ड
समीकरण x2=x0+u2t+12at2
=200+30t+12(−10)t2
=200+30t−5t2……….ii
जब पत्थर जमीन से टकराता है तब
x2=0
∴0=200+30t−5t2
अथवा t2−6t−40=0
अथवा t2−10t+4t−40=0
t(t−10)+4(t−10)=0
अथवा (t−10)(t+4)=0
अथवा t=10s
अथवा t=−4s
परंतु t=−4s सम्भव नहीं है
∴ जमीन से टकराने में लगा समय t=10s
अब समीकरण (i) में से समीकरण (ii) को घटाने पर
x2−x1=15t…………..iii
(x2−x1) दूसरे पत्थर की पहले पत्थर के सापेक्ष स्थिति को प्रदर्शित करती है।
दूसरे पत्थर का पहले पत्थर के सापेक्ष वेग
u21=u2−u1
=30−15=15 मीटर/सेकण्ड
∴ समय t=8s पर दोनों पत्थरों के बीच की दूरी
x2−x1=15x8 [समीकरण (iii)]
=120 मीटर
समीकरण (iii) एक सरल रेखा का समीकरण है। अतः ग्राफ का t=s तक भाग OA एक सरल रेखा है समय t=8s पर पहला पत्थर जमीन से टकराता है इस समय दोनों पत्थरों के बीच की दूरी (x2−x1) अधिकतम अर्थात 120 मीटर है।
8s बाद केवल दूसरा पत्थर गति में है।
दूसरे पत्थर के लिए
x2−x1=x0+u21t+12at2
=200+15t−12(−10)t2
=200+15t−5t2
यह एक परवलय का समीकरण है। अतः ग्राफ का परतलयकार भाग AB दूसरे पत्थर का पहले पत्थर के सापेक्ष 8s से 10s तक सापेक्ष स्थिति को प्रदश्रित करता है।
अतः दिया गया ग्राफ दूसरे पत्थर की पहले पत्थर के सापेक्ष स्थिति-समय ग्राफ को पूर्णतः प्रदर्शित करता है।
Topper's Solved these Questions
Similar Questions
नीचे दिए गये गति के कौन से उदाहरणों में वस्तु को लगभग बिंदु वस्तु माना जा सकता है?
(i)दो स्टेशनों के बीच बिना किसी झटके के चल रही कोई रेलगाड़ी
(ii) किसी वृत्तीय पथ पर साइकिल चला रहे किसी व्यक्ति के ऊपर बैठा कोई बंदर।
(iii) जमीन से टकराकर तेजी के मुड़ने वाली क्रिकेट की कोई फिरती गेंद।
(iv) किसी मेज के किनारे से फिसलकर गिरा कोई बीकर।
View Solutionसमतापीय प्रक्रम में क्या स्थिर रहता है?
View Solutionएक 5 मीटर का लड़का 2 मीटर त्रिज्या के क्षैतिज व्रत में एक प्रथर को डोरी से बांधकर, एकसमान्य चाल से घुमा रहा है व्रत की स्पर्श रेखा के अनुदिश चलते हुवे पृथ्वी पर 10 मीटर की क्षितिज दुरी पर गिरता है वृतीय गति में पत्थर पर कार्यरत अभिक्रिया त्वरण का मान ज्ञात कीजिय ( g = 10 मीटर/सेकण्ड2)|
View Solutionएक 13 मीटर लम्बी सीढ़ी दीवार के सहारे झुकी हुई है। सीढ़ी के पाद को 1.5 मी./से. की दर से जमीन के सारे दीवार से दूर खींचा जाता है। सीढ़ी तथा जमीन के मध्य का कोण किस गति से परिवर्तित हो रहा है जबकि सीढ़ का पावि दीवार से 12 मीटर दूर हो ।
View Solutionग्राफ की सहायता से गति के समीकरणों को व्युत्पन्न करना
View Solutionएक वस्तु पूर्व दिशा की ओर 30 मी/से के वेग से जा रही है। 10 सेकण्ड के बाद यह वस्तु 40 मी/से के वेग से उत्तर की ओर गति करती है। वस्तु का औसत त्वरण है-
View Solutionजल के अणु के विलोपन के साथ ऐल्कोहॉल और एक अम्ल के बीच की अभिक्रिया को कहा जाता है
View Solutionसंगलित अशुद्ध धातु को लकड़ी के हरे रंग के लट्टे के साथ हिलाकर फफोलेदार तांबा को परिष्कृत किया जाता है, क्योंकि इस प्रकार की लकड़ी, हाइड्रोकार्बन गैसों (जैसे CH_4 ) को मुक्त करती है। इस प्रक्रम X को ________ कहा जाता है और इसका उपयोग धातु में प्रारंभ में उपस्थित Y की अशुद्धियों के शुद्धिकरण के लिए किया जाता है। Y _______ है।
View Solutionग्लूकोज के ताजा तैयार विलयन से समय के साथ प्रकाशिक घूर्णन में परिवर्तन को निम्न में जाना जाता है -
View Solutionऑक्सीरेन की संरचना
 है।
है।
जल-अपघटन के बाद RMgX के साथ ऑक्सीरेन की अभिक्रिया से कौन सा उत्पाद विरचित होगा?
View Solutionगैस के दाब के साथ ठोस की सतह पर गैसों के अधिशोषण के लिए निम्नलिखित में से सही परिवर्तन है
View Solutionजल के अणु के विलोपन के साथ ऐल्कोहॉल और एक अम्ल के बीच की अभिक्रिया को कहा जाता है
View Solutionनिम्नलिखित में से कौनसा आरेख एक प्रबल विद्युत अपघट्य के लिए तनुकरण के साथ तुल्यांकी चालकत्व (A) की सही परिवर्तनशीलता को प्रदर्शित करता है?
View Solutionबेन्जैल्डिहाइड बनाने के लिए AlCl3 की उपस्थिति में बेन्जीन के साथ CO+HCI की अभिक्रिया को क्या कहा जाता है?
View SolutionNaOH की उपस्थिति में, फीनॉल के साथ बेंजॉयल क्लोराइड की अभिक्रिया को कहा जाता है:
View Solutionअभिक्रिया A→ उत्पाद के लिए, यह पाया गया है कि अभिक्रिया की दर 6.25 के गुणक से बढ़ जाती है, जब A की सांद्रता 2.5 के गुणक से बढ़ाई जाती है। A के संबंध में अभिक्रिया की कोटि क्या है?
View Solution
