दो समान परिमाण के वेक्टरो के योग का परिमाण कब-(a) शून्य हो सकता है, (b) प्रत्येक के बरारबर हो सकता है ?
समान परिमाण A वाले दो वेक्टरो का परिणामी
R=√A2+A2+2A⋅Acosθ=√2A2(1+cosθ)
(a) R=0 होने के लिए
1+cosθ=0 अथवा cosθ=−1
अथवा θ=180∘
(b) R=A होने के लिए
2(1+cosθ)=1 अथवा cosθ=−12
अथवा θ=120∘
Topper's Solved these Questions
- सदिश विश्लेषण BOOK - BALAJI PUBLICATIONCHAPTER - सदिश विश्लेषण EXERCISE - अभ्यास के लिए प्रश्न
11 Videos
- सदिश विश्लेषण BOOK - BALAJI PUBLICATIONCHAPTER - सदिश विश्लेषण EXERCISE - प्रश्नावली (ज्ञान परिक्षण पर आधारित प्रश्न)
35 Videos
- वृत्तीय गति की गतिकी BOOK - BALAJI PUBLICATIONCHAPTER - वृत्तीय गति की गतिकी EXERCISE - NCERT (पाठ्य - पुस्तक के प्रश्न)
54 Videos
- समतल में गति BOOK - BALAJI PUBLICATIONCHAPTER - समतल में गति EXERCISE - पाठ्य - पुस्तक के प्रशन
56 Videos
Similar Questions
यदि →A=2ˆi+5ˆj−4ˆk हो तो ज्ञात कीजिये
→A का परिमाण, (ii) X,Y,Z-अक्ष के साथ →A का कोण
View Solutionसदिश और अदिश में अन्तर लिखिए
View Solutionएकसमान चाल से नीचे गिरती वर्षा की कोई बूँद पर कार्यरत नेट बल का परिमाण व उसकी दिशा लिखिये ।
( बल F = ma अर्थात् किसी अत्वरित कण पर कार्यरत् बल शून्य होता हैं । (∵,a=0,∴F=0 ))
View Solutionनिम्नलिखित भौतिक राशियों में से बतलाइये की कोन - सी सदिश है और कोन - सी अधिश --- आयतन, द्रव्यमान, चाल, त्वरण, घटाव, मोल, संख्या, वेग, कोणीय आकृति, विस्थापन, कोणीय वेग ?
View Solutionक्या दो संख्याओं का म.स. (H.C.F.) तथा ल.स. (L.C.M)समान हो सकता है ? कारण दीजिये।
View Solution→a,→b,→c क्रमश 3,4,5 परिमाण के सदिश है। यदि प्रत्येक सदिश अन्य दो सदिशो के योग पर लम्ब हो, तो सदिश →a+→b+→c का परिमाण ज्ञात किजिए।
View Solutionयदि एक द्वितीय क्रम के सारणिक का प्रत्येक अवयव शून्य या एक हो तो सारणिक का मान धनात्मक होने की क्या प्रायिकता है ? ( यह मानते हुए कि सरणिक के प्रत्येक अवयव को स्वतंत्र रूप से चुना जा सकता है तथा प्रत्येक के चुने जाने कि प्रायिकता 12 है । )
View Solutionदो अशून्य संख्याओं का योग 8 है। उनके व्युत्क्रमों के योग का निम्निष्ठ मान है
View Solutionश्यामला केवल उन्हीं प्रश्नों के उत्तर लिखती है जो उसने याद किए होते हैं। इसका कारण हो सकता है:
View Solutionभाषा का पोर्टफोलियो हो सकता है
View Solutionबोलना-कौसल' के विकास के लिए सबसे अधिक महत्वपूर्ण सिध्द हो सकता है
View Solutionसदिश राशियो का परिमाण कैसे निकाले #!#सदिश योग के नियम व उस पर आधारित प्रश्न
View Solutionनिम्नलिखित में से किस के लिए वांट हॉफ गुणांक इकाई से अधिक नहीं हो सकता है?
View Solution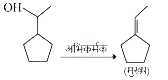
दी गयी अभिक्रिया के लिए सबसे उपयुक्त अभिकर्मक हो सकता है -
View Solutionधातु कार्बाइड, H2O के साथ अभिक्रिया पर CH4 का निर्माण करता है, कार्बाइड हो सकता है:
View Solutionसामान्य सूत्र C_n H_(2n) O_2 , कौन सी खुली श्रृंखला के लिए हो सकता है?
View Solution
