दो घर्षणरहि आनत पथ, जिनमे से एक कि ढाल अधिक है और दूसरे कि ढाल काम है, बिन्दु A पर मिलते है। बिन्दु A से प्रत्येक पथ पर एक-एक पत्थर को विरामावस्था से निचे सरकाया जाताहै (चित्र)। क्या ये पत्थर एक ही समय पर निचे पहुँचेगे? क्या वे वहाँ एक ही चाल से पहुँचेगे ? व्याख्या कीजिए। यदि $θ_{1}, = 30^{\circ}, θ_{2} = 60^{\circ}$ और h=10 मीटर दिया है तो दोनों पथरो कि चाल एव उनके द्वारा निचे पहुँचने के लिये गये समय क्या है ?

Video Solution

Text Solution

Verified by Experts

माना AB तथा AC घर्षणरहि दो आनत तल जो क्रमशः $θ_{1}$ तथा $θ_{2}$ कोण पर झुके है। AB उत्तरोत्तर पथ है तथा AC निम्नोत्तर पथ है।
माना $m_{1}$ और $m_{2}$ द्रव्यमान के दो पत्थर विरामावस्था से निचे कि और फिसलना आरम्भ करते है।

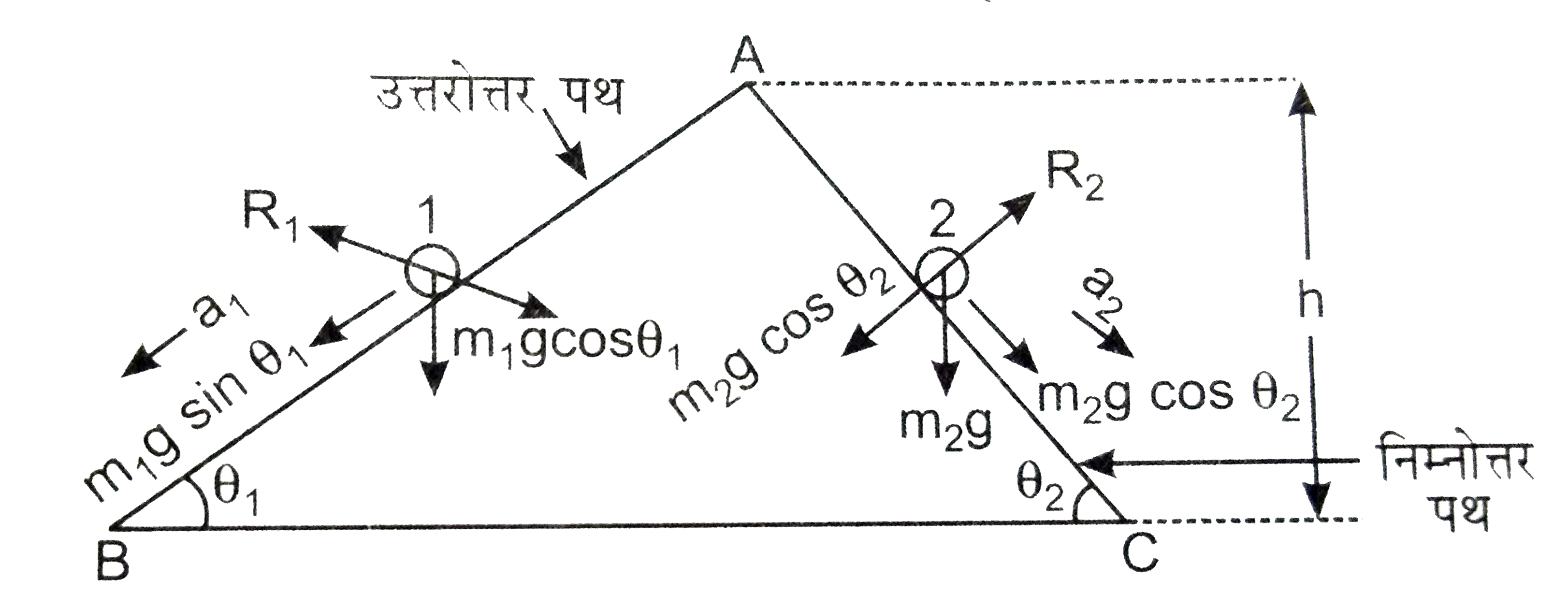
प्रत्येक तल पर A बिन्दु कि ऊँचाई A =10 मीटर विभिन्न बल प्रत्येक पत्थर पर कार्य करते है।
(i) पत्थर का भार (mg) जो ऊर्ध्वार्धरत:, निचे को कार्य करता है अपने दोनों अवयवों शेतृंज घातक $m g cos θ$ तथा उर्ध्वाधर घटक $m g sin θ$ में विभाजित हो जाता है।
(ii) अभिलम्ब प्रतिक्रिया जो तल के लंबवत है।
माना दो पत्थर के तलो तक पहुँचने में वेग $v_{1}$ तथा $v_{2}$ है। ऊर्जा संरक्षण के सिद्धांत अनुसार,
स्थितिज ऊर्जा में कमी = गतिज ऊर्जा में वृद्धि
पहले पत्थर के लिए,
$m_{1} g h = \frac{1}{2} m_{1} v_{1}^{2}$ या $v_{1} = \sqrt{2 g h}$
दीसरे पत्थर के लिए,
$m_{2} g h = \frac{1}{2} m_{2} v_{2}^{2}$ या $v_{2} = \sqrt{2 g h}$
अतः $v_{1} = v_{2} = \sqrt{2 g h}$
दोनों पत्थर समान वेग से निचे पहुँचेगे। पत्थरो के भरो में दोनों अवयव में प्रदर्शित किये गये है। यदि $a_{1}$ तथा $a_{2}$ दोनों पत्थरो के त्वरण हो, तो उनके भार के क्षैतिज घटक क्रमशः $m_{1} g {cos θ}_{1}$ तथा $m_{2} g {cos θ}_{2}$ होंगे तथा भार के यह क्षैतिज घातक अभिलम्ब प्रतिक्रिया $R_{1}$ तथा $R_{2}$ के द्वारा सन्तुलित रहते है।
पत्थरो पर लगे कुल बल $m_{1} g {sin θ}_{1}$ तथा $m_{2} g {sin θ}_{2}$ है जो निचे कि और कार्य करते है तथा या बल इन बालो के कारन पत्थर गति करते है।
$m_{1} a_{1} = m_{1} g {sin θ}_{1}$
या $a_{1} = g {sin θ}_{1}$
इसी प्रकार, $m_{2} a_{2} = m_{2} g {sin θ}_{2}$
या $a_{2} = g {sin θ}_{2}$ और $θ_{2} = 30^{\circ}$
तथा $θ_{1} = 60^{\circ}$
$∴ a_{1} = g {sin 30}^{\circ}$ =gxx1/2=g/2 $< b r > त थ ा$ a_(2)gta_(1) $य ा$ (a_(2))/(a_(1))gt1 $< b r > ग त ि क ी स म ी क र ण स े,$ v=u+at $अ थ व ा$ v=0+at $< b r >$ (u=0 $क ् य ो क ि द ो न ो ं प त ् थ र व ि र ा म ा व स ् थ ा म े ं ह ै) < b r > य ा$ v=at $< b r > य ा$ a=v/t $< b r > च ू ँ क ि द ो न ो ं प त ् थ र स म ा न व े ग स े त ल प र प ह ु ँ च त े ह ै इ स ल ि य े व े ग न ि य त ह ै । < b r >$ thereforeaprop1/t $य ा$ tprop1/a $< b r >$ therefore(t_(1))/(t_(2))=(a_(2))/(a_(1)) $< b r > ल े क ि न,$ (a_(2))/(a_(1))gt1 $< b r >$ therefore(t_(1))/(t_(2))gt1 $< b r > य ा$ t_(1)gtt_(2)
अतः दूसरे पत्थर से तल पर पहुँचने में कम समय लेगा।

|

Class 11 PHYSICS WORK, ENERGY AND POWER

Topper's Solved these Questions

Similar Questions

BALAJI PUBLICATION-कार्य, ऊर्जा, शक्ति एव संघट्ट -अतिरिक्त अभ्यास

Home
Ask Doubt
Profile