(A) दो बिंदु आवेश क्रमश: +5×10−19C तथा +10×10−19C, 1 मीटर की दुरी पर स्थित है। दोनों आवेशों को जोड़ने वाली रेखा के किस बिंदु पर वैधुत क्षेत्र शून्य होगा?
(B) यदि +10×10−19C के स्थान पर −10×10−19C आवेश रख दे तो दोनों आवेशों को मिलाने वाली रेखा के किस बिंदु पर वैधुत क्षेत्र शून्य होगा?

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

(A) किसी बिंदु पर वैधुत क्षेत्र शून्य होने के लिए उस बिंदु पर दोनों आवेशों के कारण वैधुत क्षेत्र की तीव्रता परिमाण में बराबर तथा दिशा मे विपरीत होनी चाहिए। चूँकि दोनों आवेश समान प्रकृति के है, अंत: वह बिंदु इनके बिच में होगा।
मन बिंदु P पर वैधुत क्षेत्र शून्य है (चित्र)। माना P की प्रथम आवेश से दुरी x है, अंत: दूसरे आवेश से P की दुरी (1-x) होगी। यदि 5×10−19C तथा 10×10−19C आवेश के कारण बिंदु P पर वैधुत क्षेत्र की तीव्रता क्रमश: →E1 तथा →E2 हो तो P पर वैधुत क्षेत्र शून्य होने के लिए,
→E1+→E2=0 अथवा →E1=−→E2
इनके परिमाण, E1=E2
14πε0⋅5×10−19x2=14πε0⋅10×10−19(1−x)2
(1−x)2=2x2
1−x=±√2=±1.41x
x=0.41 अथवा −2.43
x का मान ऋणात्मक नहीं होगा, अंत:
x=0.41 मीटर
अंत: वह बिंदु दोनों आवेश के बिछ में, पहले आवेश से 41 सेमि की दुरी पर होगा।
(B) दोनों आवेश विपरीत प्रकृति के है, अंत: वह बिंदु आवेशों को मिलाने वाली रेखा पर आवेशों से बहार की ओर छोटे आवेश के निकट होगा (चित्र)।
भाग (A) की भाँति हल करने पर,
E1=E2
14πε0⋅5×10−19x2=14πε0⋅10×10−19(1+x)2
(1+x)2=2x2
1+x=±x√2=±1.41x
x=2.43 अथवा −0.41
x का मान धनात्मक होगा, अंत: x=2.43 मीटर। अंत: वह बिंदु प्रथम आवेश से 2.43 मीटर दुरी पर दूसरे आवेश के विपरीत दिशा में होगा।
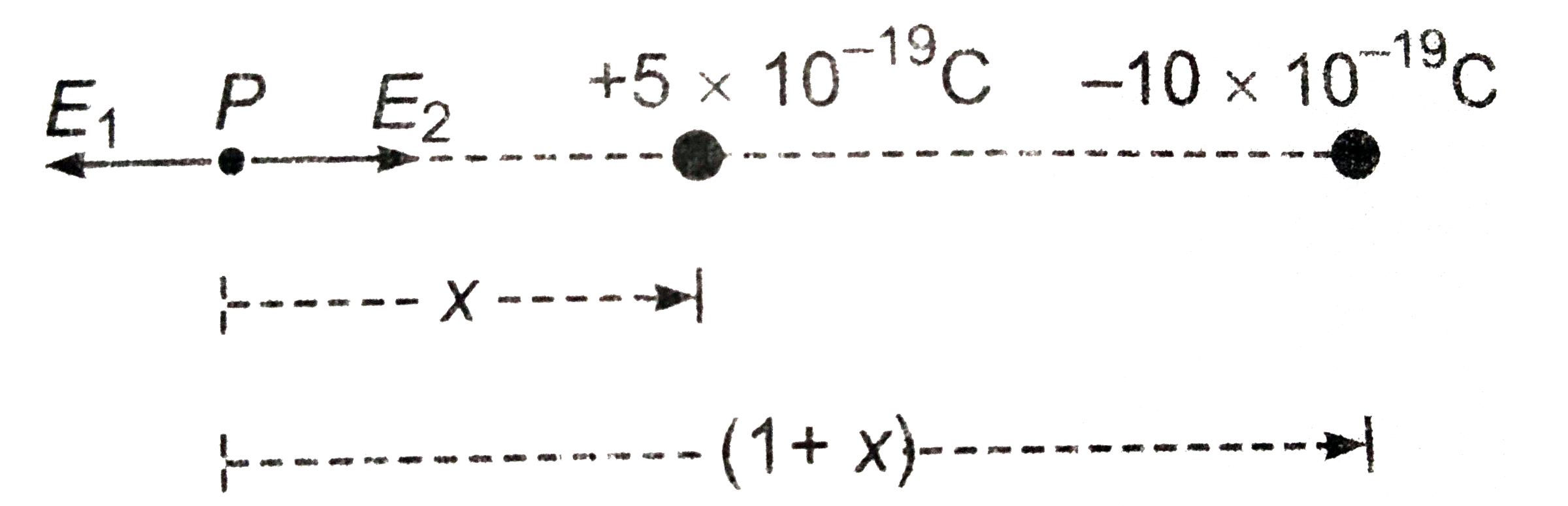
ocr_image
ocr_image

Updated on:21/07/2023
|
Class 12PHYSICSELECTROSTATICS

Topper's Solved these Questions

Similar Questions