तारों के लूप PQRSP में, जो R1 व R2 त्रिज्याओं के दो अधरवरित्कार तारों को जोड़कर बना हैं, धारा i बहती हैं। केंद्र c पर चुंबकीय क्षेत्र कि तीव्रता तथा दिशा ज्ञात कीजिये।
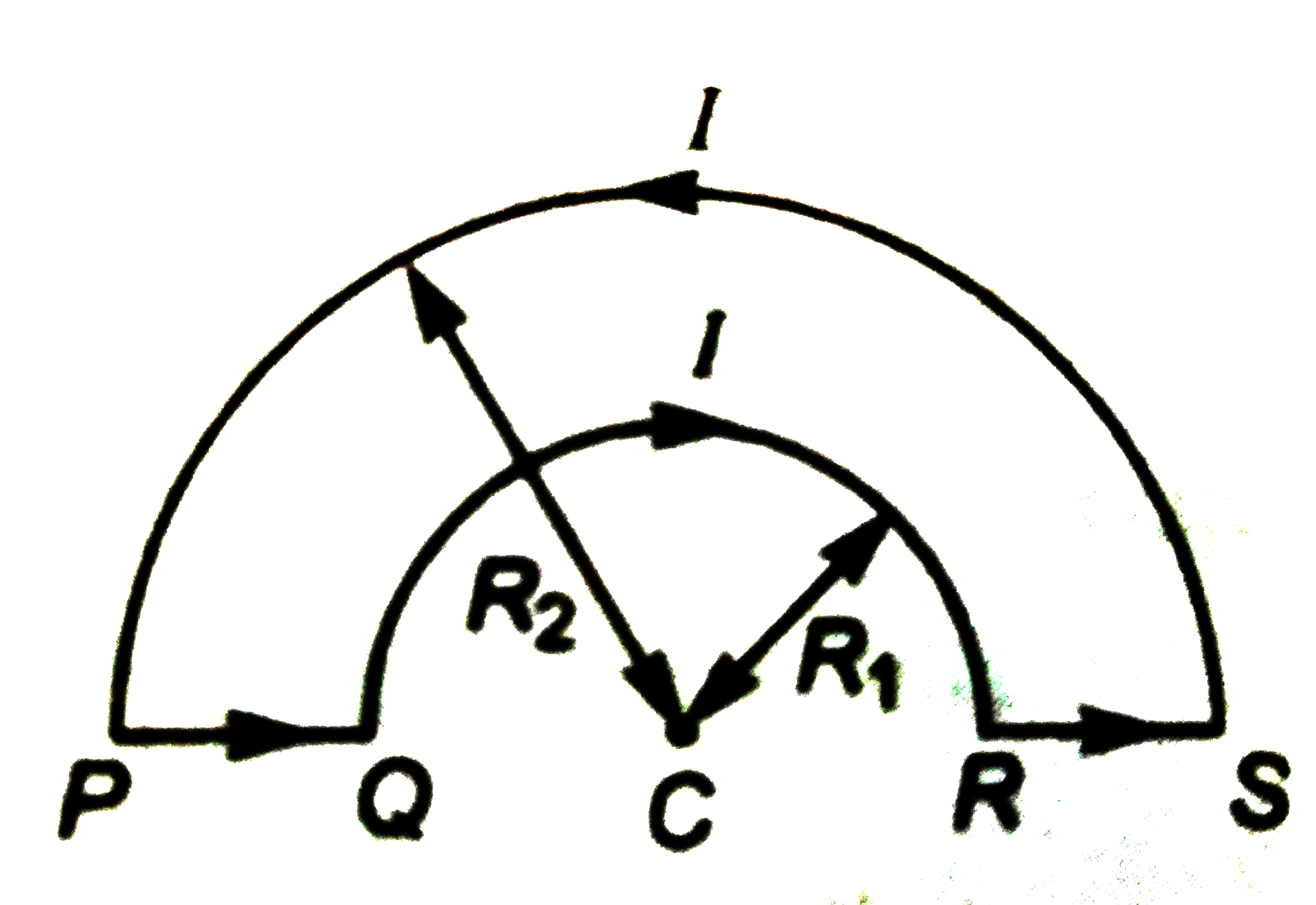
तार के सीधे भागों PQ व RS के कारण केंद्र C पर चुंबकीय क्षेत्र शून्य होगा।
R1 त्रिज्या के अर्धवृत्तकार तार के कारण C पर चुंबकीय क्षेत्र
B1=12μ0I2R1=μ0I4R1⊗
इसी प्रकार, R2 त्रिज्या के अर्धवृत्ताकार तार के कारण C पर चुंबकीय क्षेत्र
B2=μ0I4R2⊙
चूँकि B1 व B2 परस्पर विपरीत दिशा में हैं तथा B1>B2,अतः C पर परिणामी क्षेत्र
B=B1−B2=μ0I4R1−μ0I4R2=μ0I4[1R1−1R2]
B कि दिशा कागज के तल के लंबवत नीचे कि ओर हैं।
Topper's Solved these Questions
- गतिमान आवेश और चुंबकत्व Book:BALAJI PUBLICATIONChapter:गतिमान आवेश और चुंबकत्व Exercise:बहुविकल्पीय प्रशन
Explore 75 Videos
- गतिमान आवेश और चुंबकत्व Book:BALAJI PUBLICATIONChapter:गतिमान आवेश और चुंबकत्व Exercise:NCERT पाठय-पुस्तक के हल
Explore 28 Videos
- गतिमान आवेश और चुंबकत्व Book:BALAJI PUBLICATIONChapter:गतिमान आवेश और चुंबकत्व Exercise:दीर्घ उत्तरीय प्रशन
Explore 33 Videos
- किरण प्रकाशिकी एवं प्रकाशिक यंत्र Book:BALAJI PUBLICATIONChapter:किरण प्रकाशिकी एवं प्रकाशिक यंत्र Exercise:NCERT पाठ्य-पुस्तक के हल
Explore 38 Videos
- चुम्बकत्व एवं द्रव्य Book:BALAJI PUBLICATIONChapter:चुम्बकत्व एवं द्रव्य Exercise:NCERT(पाठ्य पुस्तक के हल)
Explore 50 Videos
Similar Questions
चुंबकीय क्षेत्र का मात्रक है-
View Solutionतार की एक वृत्ताकार कुंडली में 100 फेरे है, प्रत्येक की त्रिज्या 8.0 सेमी० है और इनमे 0.40 A की विद्युत धारा प्रवाहित हो रही है। कुंडली के केंद्र पर चुंबकीय क्षेत्र का परिमाण क्या है?
View Solution_________ ने प्रयोग द्वारा सर्वप्रथम सिद्ध किया कि किसी धारावाही चालक पर चुंबकीय क्षेत्र बल लगाता है।
View Solution2.5 सेमीo साइज की कोई छोटी मोमबत्ती 36 सेमीo वक्रता त्रिज्या के किसी अवतल दर्पण से 27 सेमीo दूरी पर रखी है। दर्पण से किसी परद को कितनी दूरी पर रखा जाए कि उसका सुस्पष्ट प्रतिबिम्ब परदे पर बने। प्रतिबिम्ब की प्रकृति और साइज का वर्णन कीजिए। यदि मोमबत्ती को दर्पण की और ले जाएँ, तो परदे को किस और हटाना पड़ेगा ?
View Solutionभू-चुम्बकत्व सम्बधी निम्नलिखित प्रश्नों के उत्तर दीजिए- ) एक सदिश को पूर्ण रूप से व्यक्त करने के लिए तीन राशियों की आवश्यकता होता है। उन तीन स्वतन्त्र राशियों के नाम लिखिए जो परम्परागत रूप से पृथ्वी के चुम्बकीय क्षेत्र को व्यक्त करने के लिए काम प्रयुक्त होती हैं।
View Solutionमाना कि X={1,2,3,4,5,6,7,8,9}, माना कि X में सम्बन्ध R1 तथा R2 इस प्रकार हैं कि R1={(x,y):x−y,3 से विभाज्य हैं,x≠y} तथा R2={(x,y):{x,y}⊂{1,4,7} या {x,y}⊂{2,5,8} या {x,y}⊂{3,6,9} जहाँ ⊂ का अर्थ उपसमुच्चय से हैं| दिखाएं कि R1=R2
View Solutionधारावाही वृत्ताकार लूप और कुंडली के केंद्र पर चुंबकीय क्षेत्र
View Solutionधारावाहिक चाप के कारण चुंबकीय क्षेत्र|वृत्ताकार पथ पर आवेश की गति के कारण केंद्र पर चुंबकीय क्षेत्र
View Solutionवृत्ताकार पथ पर आवेश की गति के कारण केंद्र पर चुंबकीय क्षेत्र|धारावाहि चाप के कारण केंद्र पर चुंबकीय क्षेत्र
View SolutionAmpere has given a theory to find the magnetic field due to current distribution. in loop धारा I_(3) के चुम्बकीय क्षेत्र में अंशदान को नहीं लेते है क्योंकि चुम्बकीय क्षेत्र पुरे लूप मे युग्मित है। एक समाक्षीय केबिल में तार की त्रिज्या a है , इसके चारो ओर के बेलनाकार सेल की आंतरिक व बाह्य त्रिज्याएँ क्रमशः b तथा c है। अंदर वाले तार में i ऐम्पियर धारा बहती है तथा बाहरी सेल में बराबर व विपरीत धारा बहती है। अक्ष से x दूरी ( x lt a) पर चुंबकीय क्षेत्र है
View Solutionधारावाही वृत्ताकार लूप और कुंडली के अक्ष पर चुंबकीय क्षेत्र
View Solutionतना में दो गाँठों के बीच के स्थान को ...... कहते हैं।
View Solutionदो अक्षरों के कितने सेटों के बीच उतने ही अक्षर हैं जितने कि शब्द ARISTOCRAT शब्द के वर्णानुक्रम में हैं -
View Solutionधारावाही तारों में चुंबकीय क्षेत्र | विभिन्न मामले
View SolutionRecap|धारावाही लूप के कारण चुंबकीय क्षेत्र|OMR|Summary
View SolutionRecap|धारावाही लूप के कारण चुंबकीय क्षेत्र|प्रश्न|OMR|Summary
View Solution