R=4KΩ तथा L=1.5 हेनरी के श्रेणी संयोजन पर एक प्रत्यावर्ती वोल्टता V(t)=15sin(2000t+60∘) लगाई गई है | प्रितपथ में धारा का शिखर मान, धारा तथा वोल्टता में कलान्तर, R पर शिखर वोल्टता , L पर शिखर वोल्टता और प्रयुक्त शक्ति की गणना कीजिए | यदि R को शून्य कर दिया जाये तो प्रयुक्त शक्ति कितनी हो जायेगी ?
दी गई समीकरण V(t)=15sin(2000t+60∘) की प्रत्यावर्ती वोल्टेज की समीकरण V=V0sin(ωt+ϕ) से तुलना करने पर,
V0=15 वोल्ट तथा ω=2000 रेडियन/सेकण्ड
परिपथ की प्रतिबाधा, Z=√R2+(ωL)2
प्रश्नानुसार, R=kΩ=4000 ओम,
ω=(2000)×(1.5)=3000 ओम,
∴ Z=√(40000)2+(30000)2=5000 ओम ltbrtgt परिपथ में धारा का शिखर मान,
i0=V0Z=155000 ऐम्पियर
धारा तथा वोल्टता में कलान्तर,
ϕ=tan−1(ωLR)=tan−1(30004000)=tan−1(0.75)
=37∘
R पर शिखर वोल्टता VR=L0R=(3×10−3)(4000)
= 12 वोल्ट
L पर शिखर वोल्टता VL=L0×L=L0ωL
=(3×10−3)(3000)
= 9 वोल्ट
परिपथ का शक्ति गुणांक,
cosϕ=RZ=40005000=0.8
परिपथ में प्रयुक्त औसत शक्ति
¯¯¯P=Vrms×irms×cosϕ
=V0√2×i0√2×cosϕ
=15√2×3×10−3√2×0.8
=18×10−3 वाट
यदि R को शून्य कर दे तब, cosϕ=RZ=0
¯¯¯P=0
Topper's Solved these Questions
- प्रत्यावर्ती धारा BOOK - BALAJI PUBLICATIONCHAPTER - प्रत्यावर्ती धारा EXERCISE - बहुविकल्पीय प्रश्न
80 Videos
- प्रत्यावर्ती धारा BOOK - BALAJI PUBLICATIONCHAPTER - प्रत्यावर्ती धारा EXERCISE - NCERT पाठ्य-पुस्तक के हल
11 Videos
- प्रत्यावर्ती धारा BOOK - BALAJI PUBLICATIONCHAPTER - प्रत्यावर्ती धारा EXERCISE - दीर्घ उत्तरीय प्रश्न
21 Videos
- परमाणुBOOK - BALAJI PUBLICATIONCHAPTER - परमाणुEXERCISE - बहुविकल्पीय प्रश्न
38 Videos
- प्रश्न पत्र BOOK - BALAJI PUBLICATIONCHAPTER - प्रश्न पत्र EXERCISE - भौतिक विज्ञान - 2090
1 Video
Similar Questions
भारत में A.C. की आवृत्ति है-
View Solutionएक 100Ω का प्रतिरोधक 220 V, 50 Hz आपूरित से संयोजित है |
(a) परिपथ में धारा का rms मान कितना है ?
(b) एक पुरे चक्र में कितनी नेट शक्ति व्यय होती है ?
View Solutionप्रत्यावर्ती धारा से आप क्या समझते है ? अज्यावक्रीय तथा ज्यावक्रीय धारा में क्या अंतर है ?
View Solutionरदरफोर्ड के α-प्रकीर्णन प्रयोग से यह निष्कर्ष निकलता है कि-
View Solutionएक पतली स्लिट द्वारा परदे पर बने विवर्तन प्रतिरूप में निम्निष्ठों की स्थिति के लिए व्यंजक प्राप्त कीजिए। विवर्तन प्रतिरूप में तीव्रता विभाजन का चित्र बनाइए।
View Solution283 v शिखर वोल्टता एवं 50HZ आवृति की एक ज्यावक्रीय वोल्टता एक श्रेणी बद्ध LCR परिपथ से जुडी है जिसमे R= 3Ω, L= 25.48mH एवं C= 796microfared है| ज्ञात कीजिये (a) परिपथ की प्रतिबाधा (b) स्रोत के सिरों के बीच लगी वोल्टता एवं परिपथ में प्रवाहित होने वाली धारा के बीच कालान्तर (c) परिपथ में होने वाला शक्ति क्षय (d) शक्ति गुणांक
माना कि पूर्व उदाहरण में वर्णित स्रोत की आवर्ती परिवर्तनशील है|(a) स्रोत कि किसी आवृति पर अनुनाद होगा| (b) अनुनाद की अवस्था में प्रतिबाधा, का धारा एवं क्षयित शक्ति की गणना कीजिए|
View Solutionकिसी p-n संधि डायोड में धारा को इस प्रकार व्यक्त किया जा सकता है-
I=I0[exp(eVkBT)−1] जहाँ I0 को उत्क्रमित संतृप्त धारा कहते हैं, V डायोड के सिरों पर वोल्टता है तथा यह अग्रदिशिक बायस के लिए धनात्मक तथा पश्चदिशिक बायस के लिए ऋणात्मक है। I डायोड से प्रवाहित धारा kB है बोल्ट्जमैन नियतांक (8.6×10−5eV/K) है तथा T परम ताप है। यदि किसी दिए गए डायोड के लिए I0=5×10−12 A तथा T = 300K है, तब 0.6V अग्रदिशिक वोल्टता के लिए अग्रदिशिक धारा क्या होगी?
View Solutionएक श्रेणी LCR परिपथ में L=10.0H,C=40μF तथा R=60Omega को 240V वोल्ट के परिवर्ती आवृत्ति के प्रत्यावर्ती धारा स्त्रोत से जोड़ा गया है । गणना कीजिए -(i ) स्त्रोत की कोणीय आवृत्ति जो परिपथ को अनुनाद की अवस्था में लाती है ,(ii ) अनुनादी आवृत्ति पर धारा , (iii ) प्रेरक के सिरों के बीच अनुनाद की दशा में वर्ग - माध्य - मूल विभव पतन ।
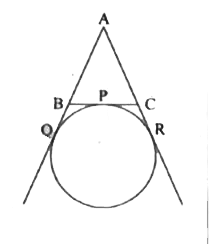
View Solutionदी गई आकृति में △ABC का बहिर्वृत्त भुजाओ को Q ,P एवं R पर स्पर्श करता है। यदि AQ=8 सेमी हो तो △ABC का परिमाप ज्ञात कीजिए।
View Solutionआकृति में PQ तथा RS एक वृत्त पर क्रमशः बिन्दु A और C पर स्पर्श रेखाएं है। यदि ∠ABC=60∘ और ∠BAP=40∘ हो तो ∠BCR ज्ञात कीजिए।

View Solutionदिष्ट धारा तथा प्रत्यावर्ती धारा || प्रत्यावर्ती धारा की विशेषताएं तथा कुछ महत्वपूर्ण पद || || वर्ग माध्य मूल मान
View SolutionRecap|विधयुत सेल |विधयुत वाहक बल तथा टर्मिनल वोल्टता |Summary
View Solutionशक्ति तथा शक्ति पर आधारित महत्वपूर्ण प्रश्न
View Solutionशक्ति तथा शक्ति पर महत्वपूर्ण प्रश्न
View Solutionकिरचाफ का वोल्टता नियम
View Solutionसेलो का विधुत वाहक बल #!#टर्मिनल वोल्टता
View Solution
