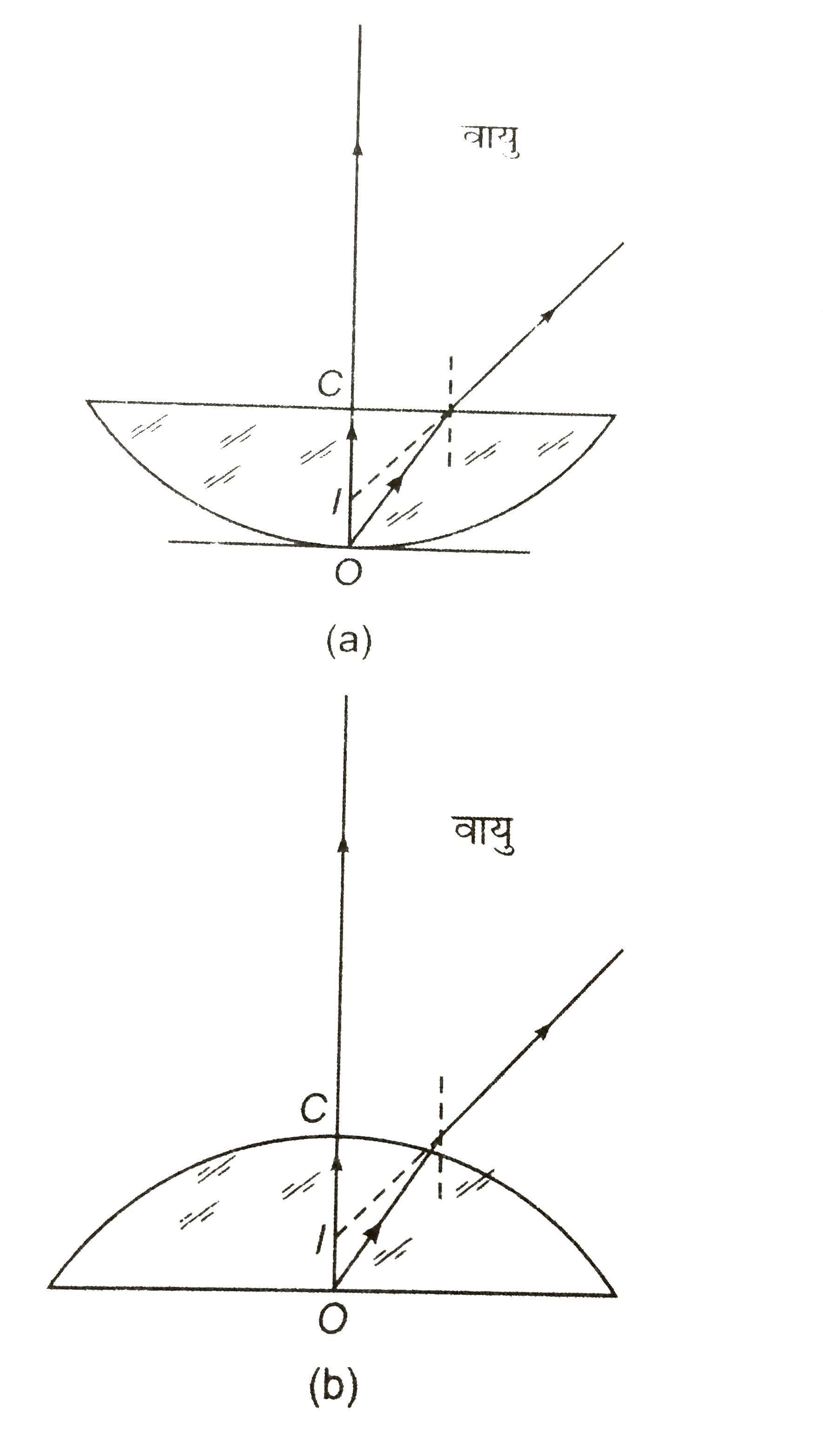
एक समतल-उत्तल लेन्स की मोटाई 4 सेमी है जब इसे एक क्षैतिज मेज पर इस प्रकार रखा जाता है कि इसका वक्र पृष्ठ मेज के सम्पर्क में रहे तो लेन्स की लेन्स की तली के बिन्दु की गहराई 3 सेमी दिखायी पड़ती है। यदि लेन्स को उलट दिया जाये जिससे समतल पृष्ठ मेज के सम्पर्क में रहे, तो लेन्स के समतल पृष्ठ के केन्द्र की आभासी गहराई 25/8 सेमी पायी जाती है। लेन्स की फोकस दूरी ज्ञात कीजिये।

Video Solution

Text Solution

Verified by Experts

प्रथम समतल स्थिति [चित्र] में माना लेन्स तथा मेज का सम्पर्क बिन्दु O है। अपवर्तन द्वारा O का आभासी प्रतिबिम्ब I बनता है। पृष्ठीय अपवर्तन के सूत्र से
$\frac{μ_{2}}{υ} - \frac{μ_{1}}{u} = \frac{μ_{2} - μ_{1}}{R}$ ……....(i)
प्रश्नानुसार, प्रकाश लेन्स से वायु में जा रहा है तथा अन्तरापृष्ठ समतल है। अतः
$μ_{1} = ?, μ_{2} = 1, R = \infty$ दिया है : $u = - 4$ सेमी,
$υ = - 3$ सेमी
समीकरण (1) में मान रखने पर
$\frac{1}{- 3} - \frac{μ_{1}}{4} = \frac{1 - 1.5}{\infty} = 0$
$\frac{μ_{1}}{4} - \frac{1}{3}$ अथवा $μ_{1} = 4 / 3$
अतः लेन्स के पदार्थ का अपवर्तनांक 4/3 है।
दूसरी स्थिति [चित्र] में
$μ_{1} = 4 / 3, μ_{2} = 1, R = ?$
$u = - 4$ सेमी,
$υ = = - 25 / 8$ सेमी
अतः समीकरण (1) से,
$\frac{1}{- 25 / 8} - \frac{4 / 3}{- 4} = \frac{1 - 4 / 3}{R}$
$\frac{- 8}{25} + \frac{1}{3} = - \frac{1}{3 R}$

$\frac{- 24 + 25}{75} = - \frac{1}{3 R}$ अथवा $R = - 25$ सेमी
अतः लेन्स की वायु में फोकस दूरी f हो तब
$\frac{1}{f} = (μ - 1) [\frac{1}{R_{1}} - \frac{1}{R_{2}}] = (\frac{4}{3} - 1) [\frac{1}{\infty} - \frac{1}{- 25}]$
$= (\frac{1}{3}) (\frac{1}{25}) = \frac{1}{75}$
अथवा $f = 75$ सेमी

Updated on:21/07/2023

|

Class 12 PHYSICS GEOMETRICAL OPTICS

Topper's Solved these Questions

Similar Questions

BALAJI PUBLICATION-किरण प्रकाशिकी एवं प्रकाशिक यंत्र -आंकिक प्रश्न

Home
Ask Doubt
Profile